如图所示为研究电子枪中电子在电场中运动的简化模型示意图．在xOy平面的第一象限，存在以x轴、y轴及双曲线y＝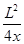
的一段(0≤x≤L,0≤y≤L)为边界的匀强电场区域Ⅰ；在第二象限存在以x＝－L、x＝－2L、y＝0、y＝L的匀强电场区域Ⅱ.两个电场大小均为E，不计电子所受重力，电子的电荷量为e，则：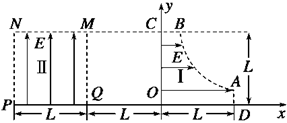
（1）求从电场区域Ⅰ的边界B点处由静止释放电子，电子离开MNPQ时的坐标；
（2）证明在电场区域Ⅰ的AB曲线边界由静止释放电子恰能从MNPQ区域左下角P点离开；
（3）求由电场区域Ⅰ的AB曲线边界由静止释放电子到达P点所需最短时间．
(12分)如图14所示，回旋加速器D形盒的半径为R，用来加速质量为m、电荷量为q的质子，使质子由静止加速到能量为E后，由A孔射出，求：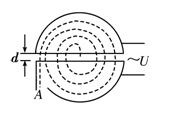
(1)加速器中匀强磁场B的方向和大小；
(2)设两D形盒间距为d，其间电压为U，电场视为匀强电场，质子每次经电
场加速后能量增加，加速到上述能量所需回旋周数；
(3)加速到上述能量所需时间．
(14分)如图12所示，在坐标系xOy中，第一象限内充满着两个匀强磁场a和b，OP为分界线，在区域a中，磁感应强度为2B，方向垂直于纸面向里；在区域b中，磁感应强度为B，方向垂直于纸面向外，P点坐标为(4l,3l)．一质量为m、电荷量为q的带正电的粒子从P点沿y轴负方向射入区域b，经过一段时间后，粒子恰能经过原点O，不计粒子重力．(sin37°＝0.6，cos37°＝0.8)求：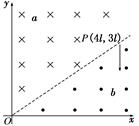
(1)粒子从P点运动到O点的时间最少是多少？
(2)粒子运动的速度可能是多少？
(12分)在电视机的设计制造过程中，要考虑到地磁场对电子束偏转的影响，可采用某种技术进行消除．为确定地磁场的影响程度，需先测定地磁场的磁感应强度的大小，在地球的北半球可将地磁场的磁感应强度分解为水平分量B1和竖直向下的分量B2，其中B1沿水平方向，对电子束影响较小可忽略，B2可通过以下装置进行测量．如图11所示，水平放置的显像管中电子(质量为m，电荷量为e)从电子枪的炽热灯丝上发出后(初速度可视为0)，先经电压为U的电场加速，然后沿水平方向自南向北运动，最后打在距加速电场出口水平距离为L的屏上，电子束在屏上的偏移距离为d.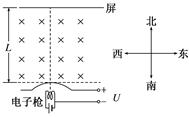
(1)试判断电子束偏向什么方向；
(2)试求地磁场的磁感应强度的竖直分量B2.
(11分)如图10所示，长为L、间距为d的平行金属板间，有垂直于纸面向里的匀强磁场，磁感应强度为B，两板不带电，现有质量为m、电荷量为q的带正电粒子(重力不计)，从左侧两极板的中心处以不同速率v水平射入，欲使粒子不打在板上，求粒子速率v应满足什么条件？、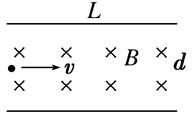 
(14分)如图12所示，匀强电场区域和匀强磁场区域是紧邻的，且宽度相等均为d，电场方向在纸平面内竖直向下，而磁场方向垂直于纸面向里，一带正电的粒子从O点以速度v0沿垂直电场方向进入电场，从A点出电场进入磁场，离开电场时带电粒子在电场方向的偏转位移为电场宽度的一半，当粒子从磁场右边界上C点穿出磁场时速度方向与进入电场O点时的速度方向一致，已知d、v0(带电粒子重力不计)，求：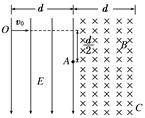
(1)粒子从C点穿出磁场时的速度大小v；
(2)电场强度E和磁感应强度B的比值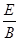
.