某物体在水平拉力F1作用下由静止开始沿水平面运动,经过时间t后,将拉力突然变为相反方向,同时改变大小为F2,又经过时间2t后恰好回到出发点,求:
(1)F1与F2之比为多少?
(2)F1与F2做功之比为多少?
(3)求t时刻与3t时刻的速率之比为多少?
一个由静止出发做匀加速直线运动的物体,在最初的3s内发生的位移是9m,试求:
(1)物体的加速度多大?
(2)第3s末物体的速度多大?
(3)第5s内物体发生的位移多大 ?
为了纪念2008年奥运会的成功举办,某公司为某游乐园设计了如图所示的玩具轨道,其中EC间的“2008”是用内壁光滑、透明的薄壁圆管弯成的竖直轨道,AB是竖直放置的光滑 圆管轨道,B、E间是粗糙的水平平台,管道B、E、C端的下表面在同一水平线上且切线均为水平方向。现让质量m=0.5Kg的闪光小球(可视为质点)从A点正上方的Q处自由落下,从A点进入轨道,依次经过
圆管轨道,B、E间是粗糙的水平平台,管道B、E、C端的下表面在同一水平线上且切线均为水平方向。现让质量m=0.5Kg的闪光小球(可视为质点)从A点正上方的Q处自由落下,从A点进入轨道,依次经过 圆管轨道AB、平台BE和“8002”后从C点水平抛出。已知
圆管轨道AB、平台BE和“8002”后从C点水平抛出。已知 圆管轨道半径
圆管轨道半径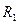 =0.4m,“O”字形圆形轨道半径
=0.4m,“O”字形圆形轨道半径 =0.02m。Q点距A点高H=5m,到达“O”字形轨道最低点P时的速度为10m/s,,取g=10m/s2。求:
=0.02m。Q点距A点高H=5m,到达“O”字形轨道最低点P时的速度为10m/s,,取g=10m/s2。求: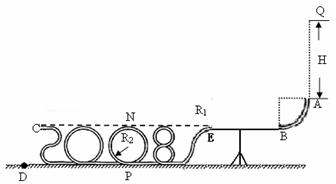
(1)小球到达O字形圆形轨道顶端N点时受到的轨道的弹力;
(2)在D点正上方高度为0.038m处设置一垂直于纸面粗细可不计的横杆,若D到C的水平距离为0.1m,则小球应距A点正上方多高处释放时,才能刚好能够从横杆上越过?
神奇的黑洞是近代引力理论所预言的 一种特殊天体,探寻黑洞的方案之一是观测双星系统的运动规律.天文学家观测河外星系大麦哲伦云时,发现了LMCX-3双星系统,它由可见星A和不可见的暗星B构成.两星视为质点,不考虑其他天体的影响,A、B围绕两者连线上的O点做匀速圆周运动,它们之间的距离保持不变,如图4
一种特殊天体,探寻黑洞的方案之一是观测双星系统的运动规律.天文学家观测河外星系大麦哲伦云时,发现了LMCX-3双星系统,它由可见星A和不可见的暗星B构成.两星视为质点,不考虑其他天体的影响,A、B围绕两者连线上的O点做匀速圆周运动,它们之间的距离保持不变,如图4 -3-5所示.引力常量为G,由观测能够得到可见星
-3-5所示.引力常量为G,由观测能够得到可见星 A的速率v和运行周期T.
A的速率v和运行周期T.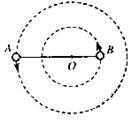
(1)可见星A所受暗星B的引力可等效为位于O点处质量为m/的星体(视为质点)对它的引力,设A和B的质量分别为m1、m2,试求m/(用m1,m2表示);
(2)求暗星B的质量m2与可见星A的速率v、运行周期T和质量m1之间的关系式;
如图所示,斜面倾角为45°,从斜面上方A点处由静止释放一个质量为m的弹性小球,在B点处和斜面碰撞,碰撞后速度大小不变,方向变为水平,经过一段时间在C点再次与斜面碰撞。已 知AB两点的高度差为h,重力加速度为g,不考虑空气阻力。求:
知AB两点的高度差为h,重力加速度为g,不考虑空气阻力。求: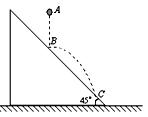
(1)小球在AB段运动过程中重力做功的平均功率P;
(2)小球落到C点时速度的大小。
质量为m=10kg的物体, 在恒定的水平外力F的作用下,沿水平面做直线运动。0~2.0s内F与运动方向相反,2.0~4.0s内F与运动方向相同,物体的速度-时间图象如图所示。(取g=10m/s2)求:
在恒定的水平外力F的作用下,沿水平面做直线运动。0~2.0s内F与运动方向相反,2.0~4.0s内F与运动方向相同,物体的速度-时间图象如图所示。(取g=10m/s2)求: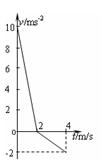
(1)水平外力F的大小
(2)水平外力F在4s内对物体所做的功。