如图所示，倾角为α的光滑斜面与半径为R＝0.4 m半圆形光滑轨道在同一竖直平面内，其中斜面与水平面BE光滑连接，水平面BE长为L＝0.4 m，直径CD沿竖直方向，C、E可看做重合。现有一可视为质点的小球从斜面上距B点竖直距离为H的地方由静止释放，小球在水平面上所受阻力为其重力的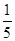
。(取g＝10 m/s2)求：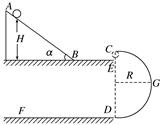
(1)若要使小球经E处水平进入圆形轨道且能沿轨道运动，H至少要有多高？如小球恰能沿轨道运动，那么小球在水平面DF上能滑行多远？
(2)若小球静止释放处离B点的高度h小于(1)中H的最小值，小球可击中与圆心等高的G点，求此h的值。
如图所示，固定于同一条竖直线上的A、B是两个带等量异种电荷的点电荷，电荷量均为Q，其中A带正电荷，B带负电荷，D、C是它们连线的垂直平分线，A、B、C三点构成一边长为d的等边三角形。另有一个带电小球E，质量为m、电荷量为＋q(可视为点电荷)，被长为L的绝缘轻质细线悬挂于O点，O点在C点的正上方。现在把小球 E拉起到M点，使细线水平绷直且与A、B、C处于同一竖直面内，并由静止开始释放，小球E向下运动到最低点C时，速度为v。已知静电力常量为k，若取D点的电势为零，试求：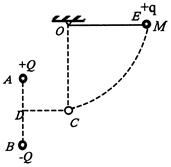
(1)在A、B所形成的电场中，M的电势φM。
(2)绝缘细线在C点所受到的拉力T 。
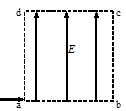
如图所示，长为L(L=ab=dc)高为H(H=bc=ad)的矩形区域abcd内存在着匀强电场。电量为q、初动能为Ek的带电粒子从a点沿ab方向进入电场，不计重力。若粒子从c点离开电场，求电场强度的大小E和粒子离开电场时的动能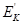
。 
质量为2kg的小球以4m/s的初速度由倾角为30°斜面底端沿斜面向上滑行，若上滑时的最大距离为1m，则小球滑回到出发点时动能为多少？（取g = 10m/s2）
半径为R的玻璃半圆柱体，横截面如图所示，圆心为O 。两条平行单色红光沿截面射向圆柱面方向与底面垂直。光线1的入射点A为圆柱面的顶点，光线 2的入射点B，∠AOB＝60°，已知该玻璃对红光的折射率n＝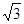
。求：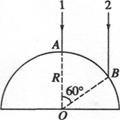
（1）两条光线经柱面和底面折射后出射光线的交点与O点的距离d；
（2）若入射的是单色蓝光，则距离d将比上面求得的结果大还是小？（定性分析，不需要计算，画出光路图）
（3）如果让一束足够宽的平行光垂直底面向上入射，则圆弧面上能射出光线的部分占圆弧部分的几分之几？
一根弹性绳沿x轴方向放置，左端在原点O，用手握住绳的左端使其沿y轴方向做周期为1 s的简谐运动，于是在绳上形成一列简谐波（如左下图）。求：
（1）若从波传到平衡位置在x=1m处的M质点时开始计时，那么经过的时间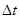
等于多少时，平衡位置在x= 4.5m处的N质点恰好第一次沿y轴正向通过平衡位置？在图中准确画出当时弹性绳上的波形。
（2）从绳的左端点开始做简谐运动起，当它通过的总路程为88cm时，求N质点振动通过的总路程和波传播的距离各为多少？