在研究微型电动机的性能时,可采用右图所示的实验电路。调节滑动变阻器,使电动机正常工作时,电压表示数为U,电流表示数为I,已知电动机的内阻为r,则当这台电动机正常运转时( )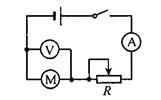
| A.电动机消耗的功率为U 2 /r |
| B.电动机消耗的热功率为UI-I2r |
| C.电动机的输入功率为UI |
| D.电动机的内阻为r=U/I |
下列说法正确的是()
| A.若物体运动速率始终不变,则物体所受合力一定为零 |
| B.若物体的加速度均匀增加,则物体做匀加速直线运动 |
| C.若物体所受合力与其速度方向相反,则物体做匀减速直线运动 |
| D.若物体在任意的相等时间间隔内位移相等,则物体做匀速直线运动 |
如图所示,置于足够长斜面上的盒子闪为放有光滑球B,B恰与盒子前、后壁接触,斜面光滑且固定于水平地面上.一轻质弹簧的一端与固定在斜面上的木板P拴接,另一端与A相连.今用外力推A使弹簧处于压缩状态,然后由静止释放,则从释放盒子直至其获得最大速度的过程中
| A.弹簧的弹性势能一直减小直至为零 |
| B.A对B做的功等于B机械能的增加量 |
| C.弹簧弹性势能的减小量等于A和B机械能的增加量 |
| D.A所受重力和弹簧弹力做功的代数和小于A动能的增加量 |
在如图所示的倾角为θ的光滑斜面上,存在着两个磁感应强度大小为B的匀强磁场,区域I的磁场方向垂直斜面向上,区域Ⅱ的磁场方向垂直斜面向下,磁场的宽度均为L,一个质量为m、电阻为R、边长也为L的正方形导线框,由静止开始沿斜面下滑,t1时 ab边刚越过GH进入磁场Ⅰ区,此时线框恰好以速度 v1做匀速直线运动;t2时ab边下滑到JP与MN的中间位置,此时线框又恰好以速度v2做匀速直线运动。重力加速度为g,下列说法中正确的有:( )
| A.t1时,线框具有加速度a=3gsinθ |
| B.线框两次匀速直线运动的速度v1: v2=2:1 |
| C.从t1到t2过程中,线框克服安培力做功的大小等于重力势能的减少量。 |
D.从t1到t2,有 机械能转化为电能。 机械能转化为电能。 |
如图,为真空中某一点电荷Q产生的电场,a、b分别是其电场中的两点,其中a点的场强大小为Ea,方向与a、b连线成120°角;b点的场强大小为Eb,方向与a、b连线成150°角。一带负电的检验电荷q在场中由a运动到b,则
A.a、b两点场强大小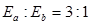 |
B.q在a、b两点受到的电场力大小之比 |
C.a、b两点电势相比较 |
D.q在a、b两点电势能相比较 |
如图所示为理想变压器原线圈所接交流电压的波形,原、副线圈匝数比n1∶n2=10∶1,串联在原线圈电路中的电流表示数为1 A,下列说法中正确的是 ( )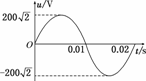
| A.变压器的输出功率为200 W |
| B.变压器的输出功率为200 W |
| C.变压器输出端的交变电流的频率为50 Hz |
| D.穿过变压器铁芯的磁通量变化率的最大值为 Wb/s |