如图所示，长为L (L=ab=dc)，高为L(L=bc=ad)的矩形区域abcd内存在着匀强电场。电量为q、质量为m、初速度为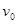
的带电粒子从a点沿ab方向进入电场，不计粒子重力。求：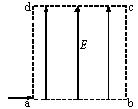
（1）若粒子从c点离开电场，求电场强度的大小；
（2）若粒子从bc边某处离开电场时速度为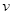
，求电场强度的大小。
如图甲所示，固定于水平面上的两根互相平行且足够长的金属导轨，处在方向竖直向下的匀强磁场中。两导轨间距离l= 0.5m，两轨道的左端之间接有一个R=0.5W的电阻。导轨上垂直放置一根质量m=0.5kg的金属杆。金属杆与导轨的电阻忽略不计。将与导轨平行的恒定拉力F作用在金属杆上，使杆从静止开始运动，杆最终将做匀速运动。当改变拉力的大小时，相对应的匀速运动速度v也会变化，v与F的关系如图乙所示。取重力加速度g=10m/s2，金属杆与导轨间的最大静摩擦力与滑动摩擦力相等，金属杆始终与轨道垂直且它们之间保持良好接触。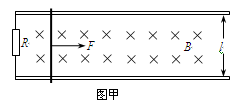
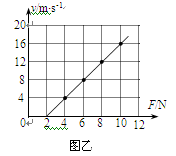
（1）金属杆在匀速运动之前做什么运动？
（2）求磁感应强度B的大小，以及金属杆与导轨间的动摩擦因数μ 。
如图甲所示，一个圆形线圈匝数n = 1000匝、面积S = 2×10-2m2、电阻r =1Ω。在线圈外接一阻值为R = 4Ω的电阻。把线圈放入一个匀强磁场中，磁场方向垂直线圈平面向里，磁场的磁感强度B随时间变化规律如图乙所示。求：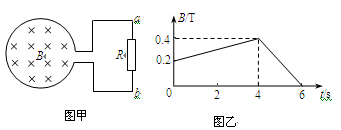
（1）0 ~ 4s内，回路中的感应电动势；
（2）t = 5s时，a、b两点哪点电势高；
（3）t = 5s时，电阻两端的电压U 。
如图所示，一矩形线圈在匀强磁场中绕OO′轴匀速转动，磁场方向与转轴垂直，磁场的磁感应强度为B。线圈匝数为n，电阻为r，长为l1，宽为l2，转动角速度为ω。线圈两端外接阻值为R的电阻和一个理想交流电流表。求：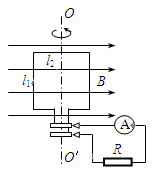
（1）线圈转至图示位置时的感应电动势；
（2）电流表的读数；
（3）从图示位置开始计时，感应电动势的瞬时值表达式。
一列简谐横波正在沿x轴的正方向传播，波速为0.5m/s，t = 0时刻的波形如图甲所示。
（1）求横波中质点振动的周期T；
（2）在图乙中画出t =1s时刻的波形图（至少画出一个波长）；
（3）在图丙中画出平衡位置为x = 0.5m处质点的振动图象（从t = 0时刻开始计时，在图中标出横轴的标度，至少画出一个周期）。
竖直平面内一光滑水平轨道与光滑曲面平滑相连.质量为m1和m2的木块A、 B静置于光滑水平轨道上，A、B之间有一轻弹簧，弹簧与木块A相固连，与木块B不固 连。将弹簧压紧用细线相连，细线突然断开，A获得动量大小为P，B冲上光滑曲面又滑下并追上A压缩弹簧，求：
①A和B的质量m1和m2的大小关系；
②B追上A并压缩弹簧的过程中弹簧的最大 弹性勢能。