如图所示为建筑工地上常用的一种“深穴打夯机”,电动机带动两个滚轮匀速转动将夯杆从深坑中提上来,当夯杆底端刚到达坑口时,两个滚轮彼此分开,将夯杆释放,夯杆在自身重力作用下,落回深坑,夯实坑底,然后两个滚轮再次压紧,夯杆被提上来,如此周而复始(夯杆被滚轮提升过程中,经历匀加速和匀速运动过程)。已知两个滚轮边缘的线速度恒为v=4m/s,滚轮对夯杆的正压力N=2×104N,滚轮与夯杆间的动摩擦因数μ=0.3,夯杆质量为m=1×103kg,坑深h=6.4m,假定在打夯的过程中坑的深度变化不大,取g=10m/s2,求: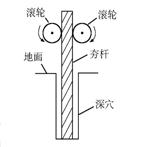
(1)夯杆被滚轮压紧,加速上升至与滚轮速度相同时的高度;
(2)每个打夯周期中,滚轮将夯杆提起的过程中,电动机对夯杆所做的功;
(3)每个打夯周期中滚轮与夯杆间因摩擦产生的热量。
如图所示,质量为m的由绝缘材料制成的球与质量为M=19m的金属球并排悬挂,摆长相同,均为l。现将绝缘球拉至与竖直方向成θ=60°的位置自由释放,摆至最低点与金属球发生弹性碰撞。在平衡位置附近存在垂直于纸面的磁场,已知由于磁场的阻尼作用,金属球总能在下一次碰撞前停在最低点处,重力加速度为g。求:
(1)第一次碰撞前绝缘球的速度v0;
(2)第一次碰撞后绝缘球的速度v1;
(3)经过几次碰撞后绝缘球偏离竖直方向的最大角度将小于37°。(你可能用到的数学知识:sin37°=0.6,cos37°=0.8,0.812=0.656,0.813=0.531,0.814=0.430,0.815=0.349,0.816=0.282)
如图所示,MNPQ是一块截面为正方形的玻璃砖,其边长MN=30 cm。一束激光AB射到玻璃砖的MQ面上(入射点为B)进入玻璃砖后在QP面上的F点(图中未画出)发生全反射,恰沿DC方向射出。其中B为MQ的中点,∠ABM=30°,PD="7.5" cm,∠CDN=30°。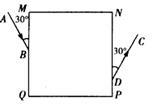
①画出激光束在玻璃砖内的光路示意图,求出QP面上的反射点F到Q点的距离QF;
②求出该玻璃砖的折射率;
③求出激光束在玻璃砖内的传播速度(真空中光速c=3×108m/s)。
图为一注射器,针筒上所标刻度是注射器的容积,最大刻度Vm=20ml,其活塞的横截面积为2cm2。先将注射器活塞移到刻度V1=18ml的位置,然后用橡胶帽密封住注射器的针孔。已知环境温度t1=27℃,大气压p0=1.0×105Pa,为使活塞移到最大刻度处,试问:(活塞质量及活塞与针筒内壁间的摩擦均忽略不计。)
(i)若把注射器浸入水中缓慢加热,水温须升至多少℃?
(ii)若沿注射器轴线用力向外缓慢拉活塞,拉力须达到多大?
如图所示,有同学做实验时不慎将圆柱形试管塞卡于试管底部,该试管塞中轴穿孔。为了拿出试管塞而不损坏试管,该同学紧握试管让其倒立由静开始竖直向下做匀加速直线运动,t=0.20s后立即停止,此时试管下降H=0.80m,试管塞将恰好能从试管口滑出。已知试管总长l=21.0cm,底部球冠的高度h=1.0cm,试管塞的长度为d=2.0cm,设试管塞相对试管壁滑动时受到的的摩擦力恒定,不计空气阻力,重力加速度g=l0m/s2。求:
(1)试管塞从静止开始到离开试管口的总位移;
(2)试管塞受到的滑动摩擦力与其重力的比值。
空间有一匀强电场,电场方向与纸面平行。一带正电、电量为q,质量为m的小球(重力不计),在恒定拉力F的作用下沿虚线以速度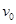 由M匀速运动到N,如图所示。已知力F和MN间夹角为
由M匀速运动到N,如图所示。已知力F和MN间夹角为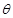 ,MN间距离为L,则:
,MN间距离为L,则:
(1)匀强电场的电场强度大小为多少?
(2)MN两点的电势差为多少?
(3)当带电小球到达N点时,撤去外力F,则小球回到过M点的等势面时的动能为多少?