课堂上老师给同学们布置了这样一个题目：假设地球是一半径为R，质量分布均匀的球体。一矿井深度为d。已知质量分布均匀的球壳对壳内物体的引力为零。求矿井底部和地球表面处的重力加速度大小之比。李明同学的思考过程如下： 由等式GM=gR2（G为引力常量，M为地球质量，R为地球半径，g为地球表面处的重力加速度）变形后得到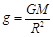
，则矿井底部的重力加速度g′与地球表面处的重力加速度g大小之比
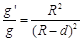。下列说法中正确的是
| A．李明的答案是正确的 |
| B．李明的答案是错误的，因为等式GM=gR2不成立 |
| C．李明的答案是错误的，因为本题不能用等式GM=gR2求解 |
| D．李明的答案是错误的，本题虽然能用等式GM=gR2求解，但他分析问题时出现错误 |
如图所示,厚薄均匀的矩形金属薄片边长ab=2bc,当将A与B接入电路或将C与D接入电路中时电阻之比RAB∶RCD为( )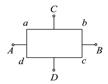
| A．1∶4 | B．1∶2 | C．2∶1 | D．4∶1 |
如图所示，当ab两端接入100V电压时，cd两端为20V；当cd两端接入100V电压时，ab两端电压为50V，则R1：R2：R3之比是（）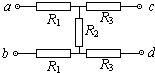
| A．3：2：1 | B．2：1：1 | C．4：2：1 | D．以上都不对 |
如图所示，4只电阻串联于某电路中，已测出UAC=9V，UBD="6" V，R2=R4，则UAE为（）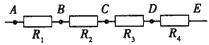
| A．3 V |
| B．7.5 V |
| C．15 V |
| D．条件不足，无法判定 |
以下给出几种电学元件的电流与电压的关系图象，如图所示，下列说法中正确的是( )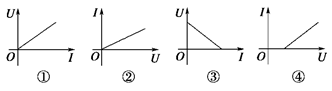
| A．这四个图象都是伏安特性曲线 |
| B．这四种电学元件都是线性元件 |
| C．①②是线性元件，③④是非线性元件 |
| D．这四个图象中，直线的斜率都表示了元件的电阻 |
用E表示电源电动势，U表示路端电压，Ur表示内电压，R表示外电路总电阻，r表示电源内电阻，I表示干路电流，则下列各式中正确的是( )
| A．Ur=IR | B．Ur=E-U | C．U=E+Ir | D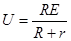． |