因为手边没有天平，小王同学思考如何利用一已知劲度系数为k的弹簧和长度测量工具来粗测一小球的质量，他从资料上查得弹簧的弹性势能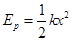
(其中x为弹簧形变量)后，设计了如下实验:将弹簧一端固定在水平桌面上，另一端紧靠小球，弹簧原长时小球恰好在桌边，然后压缩弹簧并测得压缩量x，释放弹簧，小球飞出后落在水平地面上，测出桌高h以及落点到桌边沿的水平距离s．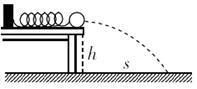
（1）小球质量的表达式为: ．
（2）如果桌面摩擦是本次实验误差的主要因素，那么小球质量的测量值将 (填“偏大”、“偏小”或“准确”)．
飞机距离地面高H=500m，水平飞行的速度为υ
=100m/s，攻击一辆速度为υ
=20m/s相向行驶的汽车，欲使投弹击中汽车，飞机应在距汽车多远处投弹？（g=10m/s
）
万有引力定律的地—月检验，假定维持月球绕地球运动的力与使得苹果下落的力是同一种力，已知地球表面重力加速度g，半径R；月球绕地球公转周期为T。月球轨道半径约为地球半径的60倍，根据牛顿定律可知月球在轨道上运动的加速度为（）。而根据月球匀速圆周运动计算出其向心加速度为( )。计算结果符合得很好，表明物体间的引力遵从相同的规律。
如左图所示，质量m=1kg的物体B置于倾角θ=37°的固定斜面上，用轻绳通过光滑的滑轮与物体A相连。t=0时同时释放A、B，物体A拉动B沿斜面向上运动，已知斜面足够长，A落地后不再反弹，物体B运动的部分v-t图如右图所示
求：（1）物体A的质量；
（2）物体B在上升过程中，和斜面摩擦产生的热量；
（3）若物体B到达最高点时，剪断绳子。取地面为零势能参考平面，物体B向下滑动过程中在何位置时具有的动能和势能相等。
如图所示，一个
圆弧形光滑细圆管轨道ABC，放置在竖直平面内，轨道半径为R，在A 点与水平地面AD相接，地面与圆心O等高，MN是放在水平地面上长为3R、厚度不计的垫子，左端M正好位于A点．将一个质量为m、直径略小于圆管直径的小球从A处管口正上方某处由静止释放，不考虑空气阻力．
（1）若小球从C点射出后恰好能打到垫子的M端，小球从C点射出时的速度；
（2）若小球从C点射出后恰好能打到垫子的M端，则小球经过C点时对细圆管的作用力；
（3）欲使小球能通过C点落到垫子上，小球离A点的最大高度。
银河系的中心可能存在大黑洞，他们的根据是用口径为3.5m的天文望远镜对猎户座中位于银河系中心附近的星体进行近六年的观测所得的数据。他们发现，距离银河系中约
km的星体正以
km/s的速度围绕银河系中心旋转。根据上面数据
求：（1）此星体的角速度；
（2）此黑洞的质量；
（3）理论分析，成为黑洞的条件是该星体的第一宇宙速度大于等于光速，此黑洞半径的最大值（引力常数是G＝6.67×10－11m3·kg－1s－2）（结果均保留一位有效数字）。