如图所示,木板长L=1.6m,质量M=4.0kg,上表面光滑,下表面与地面间的动摩擦因数为μ=0.4。质量m=1.0kg的小滑块(视为质点)放在木板的右端,开始时木板与物块均处于静止状态,现给木板以向右的初速度,取g=10m/s2,求:
(1)小滑块的加速度大小;
(2)木板的加速度大小和方向;
(3)要使小滑块从木板上掉下,木板初速度应满足什么要求。
某研究小组利用如图甲所示装置探究物块在方向始终平行于斜面、大小为F=8N的力作用下加速度与斜面倾角的关系.木板OA可绕轴O在竖直平面内转动,已知物块的质量m=1kg,通过DIS实验,得到如图乙所示的加速度与斜面倾角的关系图线.假定物块与木板间的最大静摩擦力等于滑动摩擦力,g取10m/s2.试问:
(1)图乙中图线与θ轴交点坐标分别为θ1和θ2,木板处于该两个角度时物块所受摩擦力指向何方?
(2)如果木板长L=3m,倾角为30°,若物块与木板间的动摩擦因数为 ,物块在F的作用下由O点开始运动,为保证物块不冲出木板顶端,力F最多作用多长时间?
,物块在F的作用下由O点开始运动,为保证物块不冲出木板顶端,力F最多作用多长时间?
有一炮竖直向上发射炮弹,炮弹的质量为M=6.0kg(内含炸药的质量可以忽略不计),射出时的初速度v0=60m/s。当炮弹到达最高点时爆炸为沿水平方向运动的两片,其中一片质量为m=4.0kg。现要求这一片不能落到以发射点为圆心、以R=600m为半径的圆周范围内,则刚爆炸完时两弹片的总动能至少多大?( ,忽略空气阻力)
,忽略空气阻力)
如图所示, 为一直角三棱镜的截面,其顶角
为一直角三棱镜的截面,其顶角 ,BC边长为a,棱镜的折射率为
,BC边长为a,棱镜的折射率为 ,P为垂直于直线BCO的光屏。现有一宽度等于AB的平行单色光束垂直射向AB面,求在光屏P上被折射光线照亮的光带的宽度。
,P为垂直于直线BCO的光屏。现有一宽度等于AB的平行单色光束垂直射向AB面,求在光屏P上被折射光线照亮的光带的宽度。
(已知 ;
; )
)
一圆柱形气缸,质量M为10 kg,总长度L为40 cm,内有一厚度不计的活塞,质量m为5 kg,截面积S为50 cm2,活塞与气缸壁间摩擦不计,但不漏气,当外界大气压强p0为1´105 Pa、温度t0为7°C时,如果用绳子系住活塞将气缸悬挂起来,如图所示,气缸内气体柱的高L1为35 cm,(g取10 m/s2)求:

①此时气缸内气体的压强;
②当温度升高到多少摄氏度时,活塞与气缸将分离。
如图(甲)所示,在直角坐标系0≤x≤L区域内有沿y轴正方向的匀强电场,右侧有一个以点(3L,0)为圆心、半径为L的圆形区域,圆形区域与x轴的交点分别为M、N。现有一质量为m、带电量为e的电子,从y轴上的A点以速度v0沿x轴正方向射入电场,飞出电场后从M点进入圆形区域,速度方向与x轴夹角为30°。此时在圆形区域加如图(乙)所示周期性变化的磁场,以垂直于纸面向外为磁场正方向),最后电子运动一段时间后从N点飞出,速度方向与进入磁场时的速度方向相同(与x轴夹角也为30°)。求: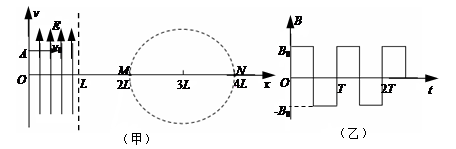
⑴ 电子进入圆形磁场区域时的速度大小;
⑵ 0≤x≤L区域内匀强电场场强E的大小;
⑶ 写出圆形磁场区域磁感应强度B0的大小、磁场变化周期T各应满足的表达式。