如图,直角梯形 中,
中, ,
, ,
, ,
, ,
, ,过
,过 作
作 ,垂足为
,垂足为 .
. 、
、 分别是
分别是 、
、 的中点.现将
的中点.现将 沿
沿 折起,使二面角
折起,使二面角 的平面角为
的平面角为 .
.

(1)求证:平面 平面
平面 ;
;
(2)求直线 与面
与面 所成角的正弦值.
所成角的正弦值.
公安部最新修订的《机动车驾驶证申领和使用的规定》于2013年1月1日起正式实施,新规实施后,获取驾照要经过三个科目的考试,先考科目一(理论一),科目一过关后才能再考科目二(桩考和路考),科目二过关后还要考科目三(理论二),只有三个科目都过关后才能拿到驾驶证,某驾校现有100名新学员,第一批参加的20人各科目通过的人数情况如下表:
| 参考人数 |
通过科目一人数 |
通过科目二人数 |
通过科目三人数 |
| 20 |
12 |
4 |
2 |
请你根据表中的数据
(1)估计该驾校这100名新学员有多少人一次性(不补考)获取驾驶证;
(2)第一批参加考试的20人中某一学员已经通过科目的一考试,求他能通过科目二却不能通过科目三的概率;
(3)该驾校为调动教官的工作积极性,规定若所教学员每通过一个科目的考试,则学校奖励教官100元,现从这20人中随机抽取1人,记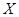 为学校因为该学员而奖励教官的金额数,求
为学校因为该学员而奖励教官的金额数,求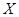 的数学期望。
的数学期望。
如图,已知函数f(x)=Asin(ωx+φ)(A>0,|φ|< )图像上一个最高点坐标为(2,2
)图像上一个最高点坐标为(2,2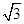 ),这个最高点到相邻最低点的图像与x轴交于点(5,0).
),这个最高点到相邻最低点的图像与x轴交于点(5,0).
(1)求f(x)的解析式;
(2)是否存在正整数m,使得将函数f(x)的图像向右平移m个单位后得到一个偶函数的图像?若存在,求m的最小值;若不存在,请说明理由.
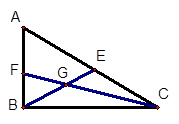
(Ⅰ)在三角形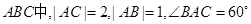 ,G是三角形
,G是三角形 的重心,求
的重心,求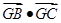 .
.
(Ⅱ)已知向量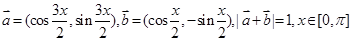 ,求x。
,求x。
如图,已知OPQ是半径为1,圆心角为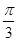 的扇形,C是扇形弧上的动点,ABCD是扇形的内接矩形,记
的扇形,C是扇形弧上的动点,ABCD是扇形的内接矩形,记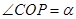 ,求当角
,求当角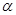 取何值时, 矩形ABCD的面积最大?并求出这个最大值.
取何值时, 矩形ABCD的面积最大?并求出这个最大值.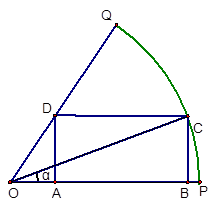
已知函数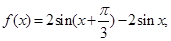

(Ⅰ)若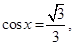 求函数
求函数 的值;
的值;
(Ⅱ)求函数 的值域。
的值域。