如图,已知矩形 中,
中,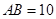 ,
, ,将矩形沿对角线
,将矩形沿对角线 把
把 折起,使
折起,使 移到
移到 点,且
点,且 在平面
在平面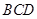 上的射影
上的射影 恰好在
恰好在 上.
上.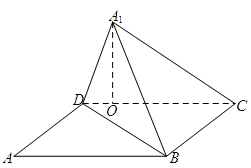
(1)求证: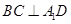 ;
;
(2)求证:平面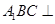 平面
平面 ;
;
(3)求三棱锥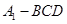 的体积.
的体积.
(本小题满分12分)如图,已知矩形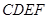 所在的平面与直角梯形
所在的平面与直角梯形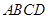 所在的平面垂直,且
所在的平面垂直,且 分别为
分别为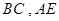 的中点.
的中点.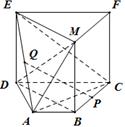
(Ⅰ)求证: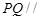 平面
平面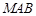 ;
;
(Ⅱ)求证:平面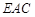 ⊥平面
⊥平面 .
.
(本小题满分12分)已知向量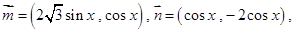 函数
函数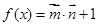 .
.
(Ⅰ)画出函数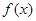 在区间
在区间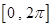 上的图象;
上的图象;
(Ⅱ)在 中,角
中,角 的对边分别是
的对边分别是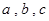 ,且满足
,且满足 求
求 的面积.
的面积.
(本小题满分14分)已知圆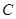 :
: 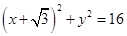 及点
及点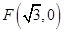 ,
,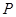 为圆
为圆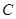 上一动点,在同一坐标平面内的动点M满足:
上一动点,在同一坐标平面内的动点M满足: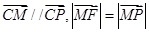 .
.
(Ⅰ)求动点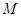 的轨迹
的轨迹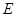 的方程;
的方程;
(Ⅱ)设过定点 的直线
的直线 与椭圆交于不同的两点
与椭圆交于不同的两点 ,且
,且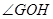 为锐角(其中
为锐角(其中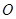 为坐标原点),求直线
为坐标原点),求直线 的斜率
的斜率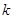 的取值范围.
的取值范围.
(Ⅲ)设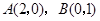 是它的两个顶点,直线
是它的两个顶点,直线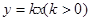 与
与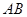 相交于点
相交于点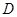 ,与椭圆相交于
,与椭圆相交于 两点.求四边形
两点.求四边形 面积的最大值
面积的最大值
(本小题满分13分)已知函数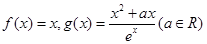 .
.
(Ⅰ)当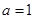 时,证明:当
时,证明:当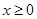 时,
时,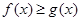 ;
;
(Ⅱ)当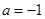 时,证明:
时,证明: .
.
(本小题满分13分)某医药公司研制了甲、乙两种抗“ABL病毒”的药物,用若干试验组进行临床对比试验.每个试验组由4位该病毒的感染者组成,其中2人服用甲种药物,另2人服用乙种药物,然后观察疗效.若在一个试验组中,服用甲种药物有效的人数比服用乙种药物有效的人数多,就称该试验组为甲类组.设每为感染者服用甲种药物有效的概率为 ,服用乙种药物有效的概率为
,服用乙种药物有效的概率为 .
.
(Ⅰ)求一个试验组为甲类组的概率;
(Ⅱ)观察三个试验组,用X表示这三个试验组中甲类组的个数,求X的分布列和数学期望.