已知数列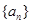 的奇数项是首项为1的等差数列,偶数项是首项为2的等比数列.数列
的奇数项是首项为1的等差数列,偶数项是首项为2的等比数列.数列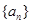 前
前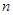 项和为
项和为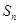 ,且满足
,且满足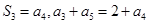
(1)求数列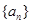 的通项公式;
的通项公式;
(2)求数列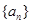 前
前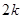 项和
项和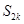 ;
;
(3)在数列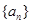 中,是否存在连续的三项
中,是否存在连续的三项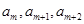 ,按原来的顺序成等差数列?若存在,求出所有满足条件的正整数
,按原来的顺序成等差数列?若存在,求出所有满足条件的正整数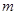 的值;若不存在,说明理由.
的值;若不存在,说明理由.
已知函数f(x)=cos(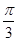 +x)·cos(
+x)·cos(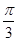 -x),g(x)=
-x),g(x)=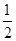 sin2x-
sin2x-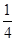 .
.
(1)求函数f(x)的最小正周期;
(2)求函数h(x)=f(x)-g(x)的最大值,并求使h(x)取得最大值的x的集合.
已知α,β∈(0,π),且tan(α-β)=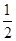 ,tanβ=-
,tanβ=-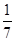 ,求2α-β的值.
,求2α-β的值.
已知函数f(x)=6cos2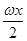 +
+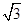 sinωx-3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B、C为图象与x轴的交点,且△ABC为正三角形.
sinωx-3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B、C为图象与x轴的交点,且△ABC为正三角形.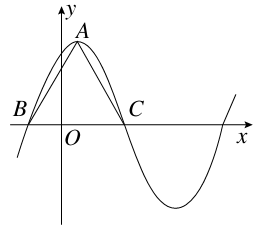
(1)求ω的值及函数f(x)的值域;
(2)若f(x0)=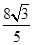 ,且x0∈(-
,且x0∈(-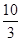 ,
,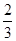 ),求f(x0+1)的值.
),求f(x0+1)的值.
已知函数f(x)=4cosωx·sin(ωx+ )(ω>0)的最小正周期为π.
)(ω>0)的最小正周期为π.
(1)求ω的值;
(2)讨论f(x)在区间[0, ]上的单调性.
]上的单调性.
已知α,β∈(0,π),且tanα=2,cosβ=-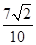 .
.
(1)求cos2α的值;
(2)求2α-β的值.