如图所示,质量为M,长度为L的小车静止的在光滑的水平面上,质量为m的小物块,放在小车的最左端,现用一水平力F作用在小物块上,使物块从静止开始做匀加速直线运动,小物块与小车之间的摩擦力为f,经过一段时间小车运动的位移为x,小物块刚好滑到小车的右端,则下列说法中正确的是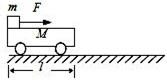
| A.物块到达小车最右端时,小车具有的动能为fx |
| B.物块和小车增加的总动能为Fx |
| C.物块克服摩擦力所做的功为f(L+x) |
| D.物块到达小车最右端时具有的动能为(F-f)(L+x) |
一质点在x轴上运动,各个时刻t(秒末)的位置坐标如下表
| t/s |
0 |
1 |
2 |
3 |
4 |
5 |
| X/m |
0 |
5 |
-4 |
-1 |
-7 |
1 |
则此质点开始运动后
A、4s内位移最大
B、第2s内位移最大
C、4s内路程最大
D、第2s内路程最大
一辆汽车以速度v行驶了全程的一半,然后匀减速行驶了一半,恰好停止,则全程的平均速度为()
A.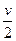 |
B.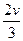 |
C.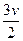 |
D.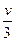 |
从地面竖直上抛物体甲,与此同时在甲的正上方有一物体乙自由下落,若两物体在空中相遇 时速率相等,则()
时速率相等,则()
| A.物体甲的初速度的大小是相遇时物体速率的2倍 |
| B.相遇时甲上升的距离是乙下落距离的2倍 |
| C.甲在空中运动时间是乙在空中运动时间的2倍 |
| D.甲落地时的速度是乙落地时速度的2倍 |
若实验中,算出各点的时刻所对应的瞬时速度,计算加速度最合理的方法是( )
A.根据实验数据画出图出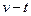 图,量出倾斜角α,由 图,量出倾斜角α,由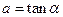 ,求出加速度 ,求出加速度 |
B.根据任意两点的速度用公式求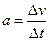 算出加速度 算出加速度 |
C.根据实验数据画出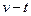 图,由图线上相距较远的两点对应的速度、时间,用公式 图,由图线上相距较远的两点对应的速度、时间,用公式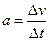 算出加速度 算出加速度 |
| D.依次算出通过连续两计数点的加速度,算出平均值作为小车的加速度 |
图2-3-8为打点计时器打出的一条纸带,从纸带上看,打点计时器出的故障是( )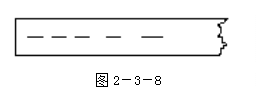
| A.打点计时器接在直流电源上 |
| B.电源电压不够大 |
| C.电源频率不稳定 |
| D.振针压得过紧 |