如图所示,用长L=0.50m的绝缘轻质细线,把一个质量 m=1.0g带电小球悬挂在带等量异种电荷的平行金属板之间,平行金属板间的距离d=5.0cm,两板间电压U=1.0×103V。静止时,绝缘线偏离竖直方向θ角,小球偏离竖直距离a=1.0cm。(θ角很小,为计算方便可认为tanθ ≈ sinθ,取g=10m/s2,需要求出具体数值,不能用θ角表示)求:
(1)两板间电场强度的大小;
(2)判断小球带何种电荷并计算其带电荷量;
(3)在图示位置,若将细线突然剪断,小球做何种性质的运动?求加速度a的大小。
(10分) 有一个质点沿x轴做单向运动,质点在各个时刻的位置坐标如下表:
| t/s |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| x/m |
2 |
4 |
6 |
8 |
8 |
8 |
12 |
17 |
20 |
24 |
求:
(1)质点在前5s内的位移;
(2)质点在第6s内的路程.
如图所示,有一条沿顺时针方向匀速传送的传送带,恒定速度v=4 m/s,传送带与水平面的夹角θ=37°,现将质量m=1kg的小物块轻放在其底端(小物块可视作质点),与此同时,给小物块沿传送带方向向上的恒力F=10 N,经过一段时间,小物块上到了离地面高为 =2.4 m的平台上。已知物块与传送带之间的动摩擦因数μ=0.5,(g取10 m/s2, sin37°=0.6,cos37°=0.8).
=2.4 m的平台上。已知物块与传送带之间的动摩擦因数μ=0.5,(g取10 m/s2, sin37°=0.6,cos37°=0.8).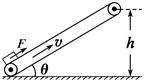
问:(1)物块从传送带底端运动到平台上所用的时间?
(2)若在物块与传送带达到相同速度时,立即撤去恒力F,计算小物块还需经过多少时间离开传送带以及离开时的速度?
如图所示,某人用轻绳牵住一只质量 =0.6kg的氢气球,因受水平风力的作用,系氢气球的轻绳与水平方向成
=0.6kg的氢气球,因受水平风力的作用,系氢气球的轻绳与水平方向成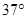 角。已知空气对气球的浮力为15N,人的质量
角。已知空气对气球的浮力为15N,人的质量 ,且人受的浮力忽略不计(sin370=0.6,cos370=0.8)。
,且人受的浮力忽略不计(sin370=0.6,cos370=0.8)。
求:(1)水平风力的大小
(2)人对地面的压力大小
(3)若水平风力增强,人对地面的压力如何变化?(要求说明理由)
一个质量m=1.0kg的物体放在粗糙的水平地面上,在水平拉力F的作用下,物体由静止开始运动,10s后拉力大小减小为F/4,并保持恒定不变。已知该物体的“速度—时间”图像如图所示。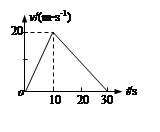
求:(1)物体所受到的水平拉力F的大小
(2)该物体与地面间的动摩擦因数
为了安全起见,在高速公路上行驶的汽车之间应保持必要的距离,有经验的司机都知道,一般高速公路的最高限速的数值(以km/h为单位)与车之间的最小间距的数值(以m为单位)差不多,如某高速公路的最高限速v=90km/h,则要求汽车间的距离至少保持90m以上。假设前方车辆因故障突然停止,后车司机从发现这一情况,经操纵刹车,到汽车开始减速需要经历一段时间即反应时间,若刹车时汽车的加速度a=4m/s2。该高速公路要求司机的反应时间至多是多少?