如图所示，在y＞0的空间中，存在沿y轴正方向的匀强电场E；在y＜0的空间中，存在沿y轴负方向的匀强电场，场强大小也为E，一电子（－e，m）在y轴上的P（0，d）点以沿x轴正方向的初速度v0开始运动，不计电子重力，求：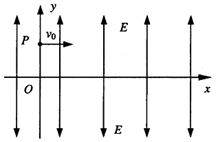
⑴电子第一次经过x轴的坐标值；
⑵请在图上画出电子在一个周期内的大致运动轨迹；
⑶电子在y方向上运动的周期；
用速度为v0、质量为m1的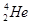
核轰击质量为m2的静止的
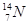核，发生核反应，最终产生两种新粒子A和B，其中A为
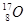核，质量为m3，速度为v3；B的质量为m4.
① 写出该反应的核方程式
② 粒子A的速度符合什么条件时，粒子B的速度方向与He核的运动方向相反．
已知光在真空中的传播速度C=3×108m/s。如图，折射率n＝1.5某玻璃立方体放在空气中。光线从立方体的顶面斜射进来，然后投射到它的另一个侧面P点，问：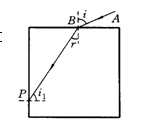
① 光在玻璃中的传播速度V；
②此光线能否从另一个侧面P点射出？请说明你判断的依据。
如图，p-T和V-T图记录了一定质量的理想气体经历了温度从200K到600K缓慢升温过程的部分变化过程。试求：
① 温度为600K时气体的压强；
② 试在p-T图上将温度从400 K缓慢升高到600 K的过程用图线表示出来。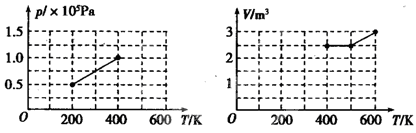
长L=0.5m的轻杆，一端固定于O点，另一端连有质量m=2kg的小球，绕O点在竖直面内作圆周运动，当它通过最高点时，求下列两种情况下，杆分别受什么力？各是多少？
（1）当V=2m/s时；
（2）当V=4m/s时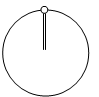
如图所示，质量为m的小球A、B分别固定在轻杆的中点和端点，当杆在光滑水平面上绕O点匀速转动时，求杆OA段与AB段对球的拉力之比。