(15分)如图甲所示，弯曲部分AB和CD是两个半径相等的1/4圆弧，中间的BC段是竖直的薄壁细圆管(细圆管内径略大于小球的直径)，分别与上下圆弧轨道相切连接，BC段的长度L可作伸缩调节，下圆弧轨道与地面相切，其中D、A分别是上、下圆弧轨道的最高点与最低点，整个轨道固定在竖直平面内，一小球多次以某一速度从A点水平进入轨道而从D点水平飞出，今在A、D两点各放一个压力传感器，测试小球对轨道A、D两点的压力，计算出压力差ΔF，改变BC的长度L，重复上述实验，最后绘得的ΔF-L图象如图乙所示。(不计一切摩擦阻力，g取10m/s2)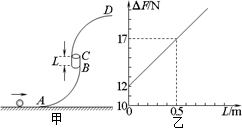
⑴某一次调节后，D点的离地高度为0.8m，小球从D点飞出，落地点与D点的水平距离为2.4m，求小球经过D点时的速度大小；
⑵求小球的质量和弯曲圆弧轨道的半径。
一棱镜的截面为直角三角形ABC，如图17所示，∠A=30o，斜边AB＝a。棱镜材料的折射率为n=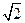 
。在此截面所在的平面内，一条光线以
的入射角从AC边的中点M射入棱镜。画出光路图，并求光线从棱镜射出点的位置（不考虑光线沿原来路返回的情况）。
渔船常利用超声波来探测远处鱼群的方位，已知某超声波频率为1.0×105 Hz，某时刻该超声波在水中传播的波动图象如图15所示．
(1)从该时刻开始计时，画出
m处质点做简谐运动的振动图象(至少一个周期)．
(2)现测得超声波信号从渔船到鱼群往返一次所用时间为4 s，求鱼群与渔船间的距离(忽略船和鱼群的运动)．
如图所示，一个有界的匀强磁场，磁感应强度B=0.50T，磁场方向垂直于纸面向里，MN是磁场的左边界．在距磁场左边界MN的1.0m处有一个放射源A，内装放射物质
（镭），发生α衰变生成新核Rn（氡）．放在MN左侧的粒子接收器接收到垂直于边界MN方向射出的α粒子，此时接收器位置距直线OA的距离为1m． 
（1）写出Ra的衰变方程；
（2）求衰变后Rn（氡）的速率（质子、中子的质量为1.6×10-27kg，电子电量e=1.6×10-19C）．
某同学为了探究质量为m1=1.0kg和m2（未知）的两个物体在光滑的水平面上正碰是否是弹性碰撞，该同学测出碰撞前后两物体的x－t（位移－时间） 图象如图所示，碰撞时间极短，试通过计算回答下列问题：
（1）质量为m1的物体在碰撞过程中动量变化量是多少?
（2）m2等于多少千克?
（3）碰撞过程是弹性碰撞还是非弹性碰撞?
如图所示的匀强电场中，有a、b、c三点，ab=5cm，bc=12cm，其中ab沿电场方向，bc和电场方向成60°角，一个电荷量为q= 4×10-8C的正电荷从a移到b电场力做功为W1=1.2×10-6J求：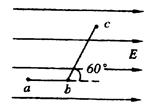
（1）匀强电场的场强E=？
（2）电荷从b移到c，电场力做功W2=？
（3）a、c两点的电势差Uac=？