一个小球从距离地面20m的高空自由下落,g取10m/s2,求
(1)小球落地时的速度大小?
(2)小球从开始运动到落地的总时间为多少?
(3)小球落地前最后1s内的位移大小?
目前我国动车组列车常使用自动闭塞法行车,自动闭塞是通过信号机将行车区间划分为若干个闭塞分区,每个闭塞分区的首端设有信号灯,当闭塞分区有车辆占用或钢轨折断时信号灯显示红色(停车),后一个闭塞分区显示黄色(制动减速),其它闭塞分区显示绿色(正常运行)。假设动车制动时所受总阻力为重力的0.1倍,动车司机可视距离为450m,不考虑反应时间。(g取10m/s2)求:
(1)如果有车停在路轨而信号系统发生故障,司机看到停在路轨上的车才开始刹车,要使动车不发生追尾,则动车运行速度不得超过多少;
(2)如果动车设计运行速度为252km/h,则
①动车的制动距离;
②正常情况下,要使动车不发生追尾,每个闭塞分区至少多长。
如图所示,倾角为30°的光滑斜面的下端与水平地面平滑连接(物体在连接处速率不变)。一个质量为m的小物体(可视为质点),从距地面h=3.2m高处由静止沿斜面下滑。物体与水平地面间的动摩擦因数为0.4 ,重力加速度g=10m/s2,求: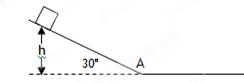
(1)物体沿斜面下滑的加速度大小;
(2)物体由静止沿斜面下滑,到达斜面底端的速度大小;
(3)物体在水平地面滑行的时间。
如图所示,玩具射击枪水平放置,玩具枪与目标靶中心位于离地面足够高的同一水平线上,枪口与目标靶中心之间的水平距离s="5" m,子弹射出的水平初速度v为10 m/s,不计空气阻力,重力加速度g为10 m/s2,(靶足够大)求: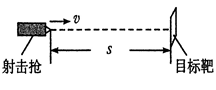
(1)从子弹由枪口射出开始计时,经多长时间子弹击中目标靶;
(2)子弹击中目标靶的位置与靶中心的距离h;
(3)子弹击中目标靶时,子弹的速度大小。
如图所示,左侧为两间距d=10 cm的平行金属板,加上电压;中间用虚线框表示的正三角形内存在垂直纸面向里的匀强磁场B1,三角形底点A与下金属板平齐,AB边的中点P恰好在上金属板的右端点;三角形区域AC右侧也存在垂直纸面向里,范围足够大的匀强磁场B2.现从左端沿中心轴线方向以v0射入一个重力不计的带电微粒,微粒质量m=1.0×10-10 kg,带电荷量q=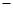 1.0×10-4 C;带电粒子恰好从P点垂直AB边以速度v=2×105 m/s进入磁场,则
1.0×10-4 C;带电粒子恰好从P点垂直AB边以速度v=2×105 m/s进入磁场,则
(1)求带电微粒的初速度v0;
(2)若带电微粒第一次垂直穿过AC,则求磁感应强度B1及第一次在B1中飞行时间;
(3)带电微粒再次经AC边回到磁场B1后,求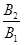 的取值在什么范围可以使带电微粒只能从BC边穿出?
的取值在什么范围可以使带电微粒只能从BC边穿出?
如图所示,一光滑绝缘圆管轨道位于竖直平面内,半径为0.2m。以圆管圆心O为原点,在环面内建立平面直角坐标系xOy,在第四象限加一竖直向下的匀强电场,其他象限加垂直于环面向外的匀强磁场。一带电量为+1.0C、质量为0.1kg的小球(直径略小于圆管直径),从x坐标轴上的b点由静止释放,小球刚好能顺时针沿圆管轨道做圆周运动。(重力加速度g取10m/s2)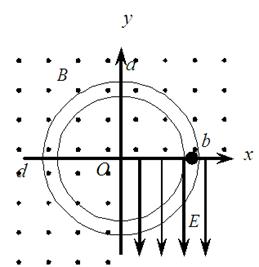
(1)求匀强电场的电场强度E;
(2)若第二次到达最高点a时,小球对轨道恰好无压力,求磁感应强度B ;
(3)求小球第三次到达最高点a时对圆管的压力。