如图所示,一个挂在绝缘细线下端的带正电的小球B,静止在图示位置,若固定的带正电的小球A的电荷量为Q,B球的质量为m,带电荷量为q,θ=30°,A和B在同一条水平线上,整个装置处于真空中,求A、B两球间的距离.(静电力常数为k,重力加速度为g)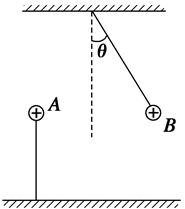
如图13(a)所示,面积S=0.2 m2的线圈,匝数n=630匝,总电阻r=1.0 Ω,线圈处在变化的磁场中,磁感应强度B随时间t按图(b)所 示规律变化,方向垂直线圈平面.图(a)中的传感器可看成一个纯电阻R,并标有“3 V,0.9 W”,滑动变阻器R0上标有“10 Ω,1 A”.试回答下列问题:
示规律变化,方向垂直线圈平面.图(a)中的传感器可看成一个纯电阻R,并标有“3 V,0.9 W”,滑动变阻器R0上标有“10 Ω,1 A”.试回答下列问题: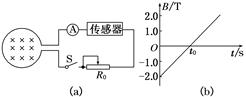
图13
(1)设磁场垂直于纸面向外为正方向,试判断通过电流表的电流方向;
(2)为了保证电路的安全,求电路中允许通过的最大电流;
(3)若滑动变阻器触头置于最左端,为了保证电路的安全,图(b)中的t0最小值是多少?
如图14甲所示,足够长的金属导轨MN和PQ与一阻值为R的电阻相连,平行
地放在水平桌面上,质量为m的金属杆ab可以无摩擦地沿导轨运动.导轨与ab杆的电
阻不计,导轨宽度为L.磁感应强度为B的匀强磁场垂直穿过整个导轨平面.现给金属杆
ab一个初速度v0,使ab杆向右滑行.回答下列问题:
图14
(1)简述金属杆ab的运动状态,并在图乙中大致作出金属杆的v-t图象;
(2)求出回路的最大电流值Im并指出金属杆中电流流向;
(3)当滑行过程中金属杆ab的速度变为v时,求杆ab的加速度a;
(4)电阻R上产生的最大热量Qm.
如图2所示,一导体圆环位于纸面内,O为圆心.环内两个圆心角为90°的扇形区域内分别有匀强磁场,两磁场磁感应强度的大小相等,方向相反且均与纸面垂直.导体杆OM可绕O转动,M端通过滑动触点与圆环良好接触.在圆心和圆环间连有电阻R.杆OM以匀角速度ω逆时针转动,t=0时恰好在图示位置.规定从a到b流经电阻R的电流方向为正,圆环和导体杆的电阻忽略不计,则杆从t=0开始转动一周的过程中,电流随ωt变化的图象是图3中的 ( )
图2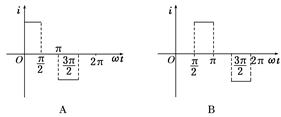
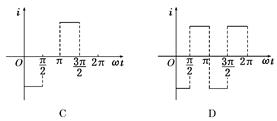
图3
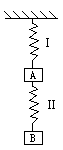
如图所示,图中弹簧Ⅰ和Ⅱ的劲度系数分别为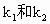 ,物体A和B的质量分别为
,物体A和B的质量分别为 .在弹性限度之内,悬挂平衡.现用一定的力沿竖直方向向上托起B,使两弹簧的长度之和恰等于两弹簧原自然长度之和.试求此时天花板对弹簧作用力F等于多大.
.在弹性限度之内,悬挂平衡.现用一定的力沿竖直方向向上托起B,使两弹簧的长度之和恰等于两弹簧原自然长度之和.试求此时天花板对弹簧作用力F等于多大.
如图所示,在水平地面上有一质量为4.0kg的物块,它与地面间的动摩擦因数μ=0.2,在与水平方向夹角为30°的斜向上的拉力F作用下,由静止开始运动。经过2.0s的时间物块发生了4.0m的位移。( g取10 m/s2)
试求:(1)物体的加速度大小;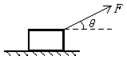 (2)拉力F的大小。
(2)拉力F的大小。