如图所示,弹簧固定在水平地面上,一小球自弹簧上端某高度h(h>0)处下落,不计空气阻力及弹簧压缩过程中的能量损失。关于此后小球运动过程,下列说法正确的是( )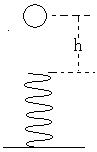
| A.小球从接触弹簧开始,到离开弹簧的过程中,速度与加速度方向先相反后相同 |
| B.小球在压缩弹簧向下运动过程中,球处于失重状态;在弹簧向上弹起小球的过程中,球处于超重状态 |
| C.小球向下运动,从接触弹簧到压缩到最低的过程中,重力势能一直减小,弹性势能一直增加 |
| D.小球仍能返回到最初的位置,小球在整个运动过程中机械能一直不变 |
如图,实线表示某电场中的电场线,M、N为电场中的两点,关于M、N两点的电场强度EM、EN的大小关系,下列说法中正确的是( )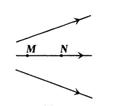
| A.EM > EN | B.EM < EN |
| C.EM = EN | D.无法判断 |
关于电场线,下列说法正确的是( )
| A.电场线方向一定是带电粒子在电场中受力的方向 |
| B.两条电场线在电场中可以相交 |
| C.电场线就是带电粒子在电场中的运动轨迹 |
| D.在同一幅电场分布图中电场越强的地方,电场线越密 |
如下图所示是电场中某区域的电场线分布图,A是电场中的一点,下列判断中正确的是()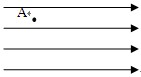
| A.A点的电场强度方向向左 |
| B.A点的电场强度方向向右 |
| C.负点电荷在A点受力向右 |
| D.正点电荷受力沿电场线方向减小 |
某电场的电场线分布如图所示,在a、 b两点,电场强度关系大小是( )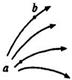
| A.a点场强强 | B.b点场强强 |
| C.a,b两点场强相等 | D.以上说法都不正确 |
对于电场线和磁感线,下列说法正确性的是( )
| A.电场线和磁感线都是闭合的曲线 |
| B.磁感线是从磁体的N极发出,终止于S极 |
| C.电场线和磁感线都不能相交 |
| D.电场线和磁感线都是现实中存在的 |