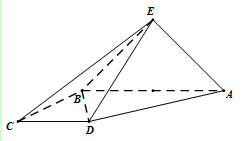
如图,四棱锥 中,面
中,面
 面
面 ,底面
,底面 是直角梯形,侧面
是直角梯形,侧面 是等腰直角三角形.且
是等腰直角三角形.且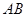 ∥
∥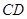 ,
, ,
,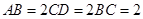 ,
,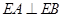 .
.
(1)判断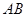 与
与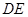 的位置关系;
的位置关系;
(2)求三棱锥 的体积;
的体积;
(3)若点 是线段
是线段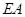 上一点,当
上一点,当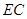 //平面
//平面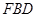 时,求
时,求 的长.
的长.
已知函数f(x)=Asin(ωx+φ)(x∈R,ω>0,0<φ<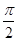 )的部分图象如图所示.
)的部分图象如图所示.
(1)求函数f(x)的解析式;
(2)求函数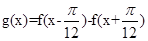 的单调递增区间.
的单调递增区间.
设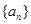 是公比大于
是公比大于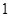 的等比数列,
的等比数列, 为数列
为数列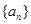 的前
的前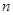 项和.已知
项和.已知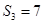 ,且
,且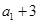 ,
,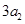 ,
,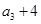 构成等差数列.
构成等差数列.
(1)求数列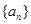 的通项公式;
的通项公式;
(2)令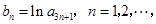 求数列
求数列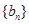 的前
的前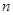 项和
项和 .
.
已知在四棱锥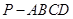 中,底面
中,底面 是矩形,且
是矩形,且 ,
, ,
,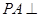 平面
平面 ,
,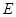 、
、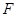 分别是线段
分别是线段 、
、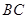 的中点.
的中点.
(1)证明: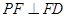 ;
;
(2)判断并说明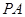 上是否存在点
上是否存在点 ,使得
,使得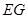 ∥平面
∥平面 ;
;
等差数列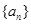 的各项均为正数,
的各项均为正数, ,前项和为
,前项和为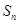 ,
, 为等比数列,
为等比数列,  ,且
,且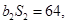
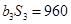 . (1)求
. (1)求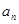 与
与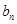 ;
;
(2)求和: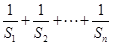 .
.
设命题p:函数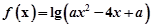 的定义域为R;
的定义域为R;
命题q:不等式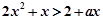 ,对
,对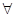
 ∈(-∞,-1)上恒成立,
∈(-∞,-1)上恒成立,
如果命题“ ”为真命题,命题“
”为真命题,命题“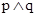 ”为假命题,求实数
”为假命题,求实数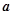 的取值范围.
的取值范围.