已知向量 ,设函数
,设函数 +1
+1
(1)若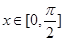 ,
,  ,求
,求 的值;
的值;
(2)在△ABC中,角A,B,C的对边分别是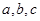 ,且满足
,且满足 ,求
,求
的取值范围.
(8分)已知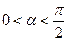 ,
, .
.
(Ⅰ)求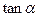 的值;
的值;
(Ⅱ)求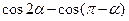 的值.
的值.
(理)已知函数f(x)= 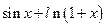
(I)求证: 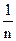 <f(
<f(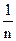 )<
)< (n∈N+)
(n∈N+)
(II)如果对任何x≥0,都有f(x)≤ax,求a的取值范围
(本小题满分14分
(文)已知函数f(x)=x3-x
(I)求曲线y=f(x)在点M(t,f(t))处的切线方程
(II)设常数a>0,如果过点P(a,m)可作曲线y= f(x)的三条切线,求m的取值范围.
(本小题满分12分)
设数列{an}的首项a1∈(0,1),an+1= (n∈N+)
(n∈N+)
(I)求{an}的通项公式
(II)设bn=an ,判断数列{bn}的单调性,并证明你的结论
,判断数列{bn}的单调性,并证明你的结论
(本小题满分12分)
已知F1(-2,0),F2(2,0),点P满足∣PF1∣-∣PF2∣=2,记点P的轨迹为E.
(I)求轨迹E的方程
(II)若直线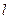 过点F2且与轨迹E交于P,Q两点.无论直线
过点F2且与轨迹E交于P,Q两点.无论直线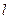 绕点F2怎样转动,在x轴上总存在定点M(m,0),使MP⊥MQ恒成立,求实数m的值.
绕点F2怎样转动,在x轴上总存在定点M(m,0),使MP⊥MQ恒成立,求实数m的值.