要得到一个奇函数,只需将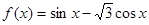 的图象( )
的图象( )
A.向右平移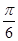 个单位 个单位 |
B.向右平移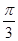 个单位 个单位 |
C.向左平移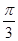 个单位 个单位 |
D.向左平移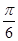 个单位 个单位 |
已知点 ,
,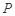 是函数
是函数 图象上不同于
图象上不同于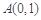 的一点.有如下结论:
的一点.有如下结论:
①存在点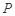 使得
使得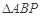 是等腰三角形;
是等腰三角形;
②存在点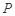 使得
使得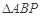 是锐角三角形;
是锐角三角形;
③存在点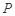 使得
使得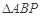 是直角三角形.
是直角三角形.
其中,正确的结论的个数为( )
| A.0 | B.1 | C.2 | D.3 |
已知函数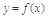 定义域为
定义域为 ,且函数
,且函数 的图象关于直线
的图象关于直线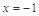 对称,当
对称,当 时,
时,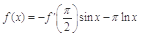 ,(其中
,(其中 是
是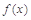 的导函数),若
的导函数),若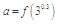 ,
,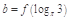 ,
,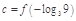 则
则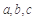 的大小关系是( )
的大小关系是( )
A.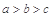 |
B.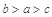 |
C. |
D.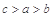 |
已知恒过定点(1,1)的圆C截直线 所得弦长为2,则圆心C的轨迹方程为( )
所得弦长为2,则圆心C的轨迹方程为( )
A. |
B.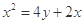 |
C. |
D.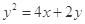 |
右图是某几何体的三视图,则该几何体的表面积等于( )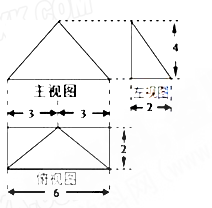
A.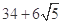 |
B.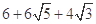 |
C.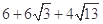 |
D. |
函数y = x 2-2x在区间[a,b]上的值域是[-1,3],则点(a,b)的轨迹是图中的( ) 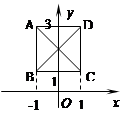
| A.线段AB和线段AD | B.线段AB和线段CD |
| C.线段AD和线段BC | D.线段AC和线段BD |