若函数
满足：在定义域内存在实数
，使
(k为常数)，则称“f（x）关于k可线性分解”．
（Ⅰ）函数
是否关于1可线性分解?请说明理由；
（Ⅱ）已知函数
关于
可线性分解，求的取值范围；
（Ⅲ）证明不等式：
．
在△ABC中，三内角A、B、C成等差数列，角B的对边b为1，求证：1＜a+c≤2.
集合A={x|x2-5x+4≤0}，B={x|x2-2ax+a+2≤0}，若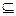B
A且B≠
，求a的取值范围.
（本小题满分10分）选修4—5：不等式选讲
(I)已知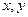
都是正实数，求证：
；
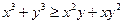(II)已知
都是正实数，求证：
.
（本小题满分10分）选修4—4：坐标系与参数方程
已知极坐标系的极点与直角坐标系的原点重合，极轴与直角坐标系的
轴的正半轴重合．直线
的参数方程是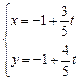
（
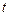为参数），曲线
的极坐标方程为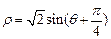
．
(I)求曲线的直角坐标方程；
(II)设直线与曲线相交于
，
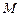两点，求M,N两点间的距离
（本小题满分10分）选修4—1：几何证明选讲
如图所示，AB是⊙O的直径，G为AB延长线上的一点，GCD是⊙O的割线，过点(
G作AB的垂线，交AC的延长线于点E，交AD的延长线于点F，过G作⊙O的切线，切点为H .求证：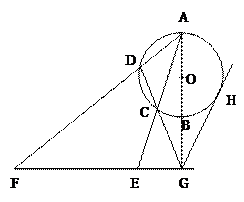
（I）C，D，F，E四点共圆；
（II）GH2=GE·GF.