如图所示,质量为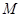
的卡车载有质量为
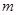的重物在平直的公路上以速率
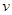前行,重物与车厢前壁距离为
.卡车紧急制动后做匀变速直线运动，车轮与地面间的动摩擦因数为
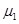，重力加速度为
.
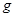（1）若重物与车厢没有相对滑动，从卡车制动开始到完全停止需要多长时间？此期间重物所受的摩擦力为多大？
（2）若重物与车厢有相对滑动，它们之间的动摩擦因数为
,为了避免制动时重物与车厢前壁发生碰撞，卡车制动前的速率最大为多少？
如图所示，在磁感应强度B＝0.2 T、方向与纸面垂直的匀强磁场中，有水平放置的两平行导轨ab、cd，其间距L＝50 cm，a、c间接有电阻R．现有一电阻为r的导体棒MN跨放在两导轨间，并以v＝10 m/s的恒定速度向右运动，a、c间电压为0.8 V，且a点电势高．其余电阻忽略不计．问：导体棒产生的感应电动势是多大？
通过导体棒电流方向如何？磁场的方向是指向纸里，还是指向纸外?
R与r的比值是多少？
把一根长L= 10cm的导线垂直磁感线方向放入如图所示的匀强磁场中，当导线中通以I1 = 2A的电流时，导线受到的安培力大小为 1.0×10－7N，则该磁场的磁感应强度为多少？
若该导线中通以I2 = 3A的电流，则此时导线所受安培力大小是多少？方向如何？
 |
如图甲所示，x轴上方有一匀强磁场，磁感应强度的方向垂直于纸面向里、大小为B，x轴下方有一匀强电场，电场强度的大小为E，方向与y轴的夹角
且斜向上方．现有一质量为m、电荷量为q的正离子，以速度
由y轴上的A点沿y轴正方向射入磁场，该离子在磁场中运动一段时间后从x轴上的C点进入电场区域，该离子经过C点时的速度方向与x轴夹角为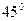
．不计离子的重力，设磁场区域和电场区域足够大．
求：
|
如图甲所示，在倾角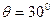
的绝缘斜面上，固定一宽
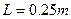的平行金属导轨，在导轨上端接入电源和滑动变阻器R，电源电动势
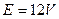，内阻
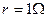，一质量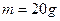
的金属棒ab与两导轨垂直并接触良好，整个装置处于磁感应强度B="0.80" T，垂直于斜面向上的匀强磁场中．金属导轨光滑，导轨与金属棒的电阻不计，取
，要保持金属棒在导轨上静止，求：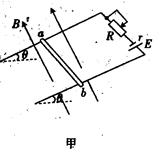
金属棒所受到的安培力．
通过金属棒的电流．
滑动变阻器R接入电路中的阻值．
一台小型电动机在3 V电压下工作，通过它的电流是0.2 A，此情况下电动机提升一重为4 N的物体，在30s内物体匀速上升了3 m．不计除电动机线圈热效应以外的其他能量损失．求在提升重物的30s内，电动机线圈所产生的热量．
若电动机的转子突然被卡住不动，则其发热的功率为多大?