如图,已知AB是⊙O的弦,OB=2,∠B=30°,C是弦AB上一点(不与点A、B重合),连结CO并延长CO交⊙O于点D,连结AD.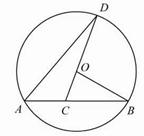
(1)求弦长AB的长度;(结果保留根号);
(2)当∠D=20°时,求∠BOD的度数.
谢老师家里收藏了2008年北京奥运会吉祥物“福娃”玩具和徽章两种商品,根据下图提供的信息,求当年谢老师买一盒“福娃”玩具和一枚徽章的价格各是多少?
如图,在正方形网格上有一个△DEF。
作△DEF关于直线HG的轴对称图形(不写作法);
作EF边上的高(不写作法);
若网格上的最小正方形边长为1,求△DEF的面积.
桌面上并排放着四张扑克牌(如图),小明和小聪一起玩抽牌游戏,两人规定:小明从前两张牌中任抽一张,小聪从后两张牌中任抽一张。(A表示的数字为1)用画树状图或列表的方法求出各种可能出现的结果;[
求两人抽到的牌面数字和为偶数的概率。

解方程组:(1)
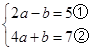
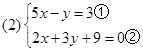
如图,ΔABC中,BM、BN三等分∠ABC,CM、CN三等分 ,
,
且 ,求
,求 的度数。
的度数。