如图所示,两平行金属板相距为d,加上如图所示(b)所示的方波形电压,电压的最大值为U0,周期为T.现有重力可忽略的一束离子,每个离子的质量为m,电量为q,从与两板等距处的O点,沿着与板平行的方向连续地射入两板中。已知每个离子通过平行板所需的时间恰为T(电压变化周期)且所有离子都能通过两板间的空间,打在两金属板右端的荧光屏上,试求: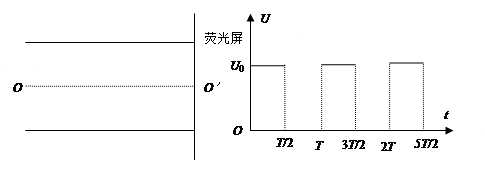
(1)离子打在荧光屏上的位置与O′点的最小距离
(2)离子打在荧光屏上的位置与O′点的最大距离。
如图所示的电路中,电阻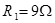 ,
, ,电源的电动势E=12V,内电阻r=1Ω,理想电流表A的读数I=0.4A。求:
,电源的电动势E=12V,内电阻r=1Ω,理想电流表A的读数I=0.4A。求: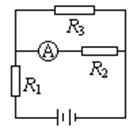
(1)电阻 的阻值
的阻值
(2)电源的输出功率
(3)电源的效率
竖直放置的两块足够长的平行金属板间有匀强电场.其电场强度为E,在该匀强电场中,用绝缘丝线悬挂质量为m的带电小球,丝线跟竖直方向成θ=30o角时小球恰好平衡,且此时与右板的距离为b,如图所示.已知重力加速度为g,求: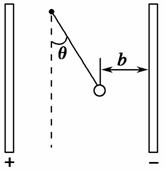
(1)小球带电荷量是多少?
(2)若剪断丝线,小球碰到金属板需多长时间?
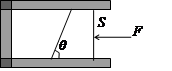
如图所示,气缸内装有一定质量的气体,气缸的截面积为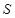 ,其活塞为梯形,它的一个面与气缸成
,其活塞为梯形,它的一个面与气缸成 角,活塞与器壁间的摩擦忽略不计,现用一水平力
角,活塞与器壁间的摩擦忽略不计,现用一水平力 推活塞,汽缸不动,此时大气压强为
推活塞,汽缸不动,此时大气压强为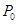 ,求气缸内气体的压强
,求气缸内气体的压强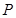 .
.
如图甲所示,固定光滑细杆与水平地面成一定倾角,在杆上套有一个光滑小环,小环在沿杆方向向上的推力 作用下向上运动。0~2s内推力的大小为5.0N,2~4s内推力的大小变为5.5N,小环运动的速度随时间变化的规律如图乙所示,重力加速度
作用下向上运动。0~2s内推力的大小为5.0N,2~4s内推力的大小变为5.5N,小环运动的速度随时间变化的规律如图乙所示,重力加速度 取10m/s2。求:
取10m/s2。求: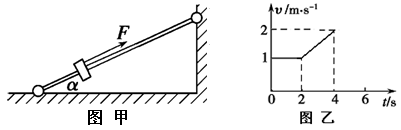
(1)小环在加速运动时的加速度 的大小;
的大小;
(2)小环的质量 ;
;
(3)细杆与水平地面之间的夹角 。
。
一个底面粗糙、质量为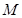 的劈放在粗糙的水平面上,劈的斜面光滑且与水平面成
的劈放在粗糙的水平面上,劈的斜面光滑且与水平面成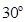 角;现用一端固定的轻绳系一质量为
角;现用一端固定的轻绳系一质量为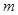 的小球,小球放在斜面上,小球静止时轻绳与竖直方向的夹角也为
的小球,小球放在斜面上,小球静止时轻绳与竖直方向的夹角也为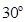 ,如图所示,试求:
,如图所示,试求:
(1)当劈静止时绳子的拉力大小。
(2)当劈静止时地面对劈的摩擦力的大小。
(3)若地面对劈的最大静摩擦力等于地面对劈支持力的k倍,为使整个系统静止,k值必须满足什么条件?