如图是一个十字路口的示意图,每条停车线到十字路中心O的距离均为20m。一人骑电动助力车以7m/s的速度到达停车线(图中A点)时,发现左前方道路一辆轿车正以8m/s的速度驶来,车头已抵达停车线(图中B),设两车均沿道路中央作直线运动,助力车可视为质点,轿车长4.8m,宽度可不计。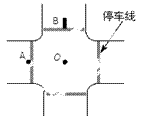
(1)请通过计算判断两车保持上述速度匀速运动,是否会发生相撞事故?
(2)若轿车保持上述速度匀速运动,而助力车立即作匀加速直线运动,为避免发生相撞事故,助力车的加速度至少要多大?
在“探究弹力与弹簧伸长的关系”的实验中关于操作步骤先后顺序,下列说法正确的是
| A.先测量原长,后竖直悬挂 |
| B.先竖直悬挂,后测量原长 |
| C.先后顺序对实验结果无影响 |
| D.先后顺序对实验结果的影响程度取决于弹簧的自重 |
学习物理除了知识的学习外,更重要的是领悟并掌握处理物理问题的思想与方法,下面几个实验是我们学习过的实验,其中研究物理问题的思想相同的是()
有同学利用如图的装置来验证力的平行四边形定则:在竖直木板上铺有白纸,固定两个光滑的滑轮A和B,将绳子打一个结点O,每个勾码的重量相等,当系统达到平衡时,根据勾码个数读出三根据绳子的拉力TOA、TOA和TOA,回答下列问题:
(1)改变勾码个数,实验能完成的是()
A.勾码的个数N1=N2=2,N3="4"
B.勾码的个数N1=N3=3,N2="4"
C.勾码的个数N1=N2=N3=4
D.勾码的个数N1=3,N2=4,N3=5
(2)在拆下勾码和绳子前,最重要的一个步骤是()
A.标记结点O的位置,并记录OA、OB、OC三段绳子的方向.
B.量出OA、OB、OC三段绳子的长度
C.用量角器量出三根绳子之间的夹角
D.用天平测出勾码的质量
(3)在作图时,你认为下图中图 是正确的.(填“甲”或“乙”)
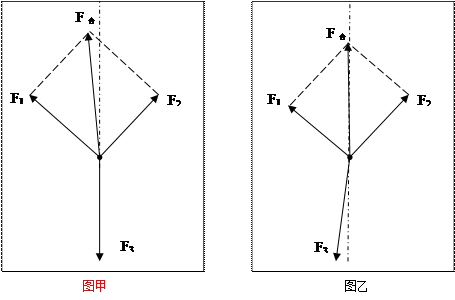 |
某同学在做探究弹力和弹簧伸长的关系的实验中,设计了如图所示的实验装置。所用的钩码每只的质量都是30g,他先测出不挂钩码时弹簧的自然长度,再将5个钩码逐个挂在弹簧的下端,每次都测出相应的弹簧总长度,将数据填在了下面的表中。(弹力始终未超过弹性限度,取g=9.8m/s2) 
试根据这些实验数据在右图给定的坐标纸上作出弹簧所受弹力大小
F跟弹簧总长L之间的函数关系图线。求该弹簧的劲度k?
(2)有一额定电压是3V,额定电流0.5A的小灯泡,为测其正常工作时的电阻,可提供的器材有:
A.电流表(量程3A,内阻0.01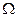 ) ) |
B.电流表(量程0.6A,内阻0.2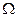 ) ) |
C.电压表(量程3V,内阻10 k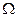 ) ) |
D.电压表(量程15V,内阻50 k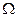 ) ) |
E.电键及导线若干
F.滑动变阻器(阻值0~10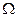 )
)
G.电源(电动势9V,内阻1 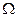 )
)
①假设用限流接法,计算通过灯泡的最小电流约__________A
②请根据上面的计算,在方框中画出用伏安法测小灯泡正常工作时电阻的电路图。
③选用的电流表是__________,选用的电压表是__________.