如图所示，AB为倾角θ＝37°的斜面轨道，轨道的AC部分光滑，CB部分粗糙。BP为圆心角等于143°，半径R=1m的竖直光滑圆弧形轨道，两轨道相切于B点，P、0两点在同一竖直线上，轻弹簧一端固定在A点,另一自由端在斜面上C点处，现有一质量m = 2kg的物块在外力作用下将弹簧缓慢压缩到D点后（不栓接）释放，物块经过C点后，从C点运动到B点过程中的位移与时间的关系为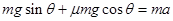
（式中x单位是m , t单位是s），假设物块笫一次经过B点后恰能到达P点，（sin 37°=0.6，cos 37°=0.8)，g取1Om/s2。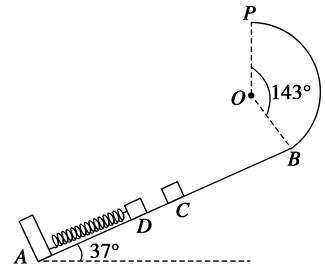
试求：（1） 若CD=1m，试求物块从D点运动到C点的过程中，弹簧对物块所做的功；
（2） B、C两点间的距离x
（3） 若在P处安装一个竖直弹性挡板，小物块与挡板碰撞时间极短且无机械能损失，小物块与弹簧相互作用不损失机械能，试通过计算判断物块在第一次与挡板碰撞后的运动过程中是否会脱离轨道？
如图所示，一质点从地面以一定的初速度竖直向上抛出，连续两次通过其上方一点P的时间为4s，已知P点距地面为10m，g=10m/s2，
求：（1）该质点抛出时的初速度
（2）该质点在运动过程中距离地面最高为多少？
（3）该质点最后1s内的位移大小。
一质点从距离地面45m的高度自由下落，重力加速度g=10m/s2，
求：
（1）质点落地时的速度
（2）下落过程中质点的平均速度
（3）最后1s内质点走过的位移大小
如图所示装置由AB、BC、CD三段轨道组成，轨道交接处均由很小的圆弧平滑连接，其中轨道AB、CD段是光滑的，水平轨道BC的长度s＝ 5 m，轨道CD足够长且倾角θ＝37°，A、D两点离轨道BC的高度分别为h1＝4.30 m、h2＝1.35 m。现让质量为m的小滑块自A点由静止释放。已知小滑块与轨道BC间的动摩擦因数μ＝0.5，重力加速度g取10 m/s2，sin 37°＝0.6，cos 37°＝0.8。求：
（1）小滑块第一次到达D点时的速度大小；
（2）小滑块第一次与第二次通过C点的时间间隔．
如图所示，足够长的传送带水平放置，以速度v=4m/s向右匀速转动，传送带上表面离地面的高度h=0.45m，一质量为m=1kg的物块，以速度v0=6m/s向左滑上传送带，与传送带之间的动摩擦因数为μ=0.2，g取10m/s2，求：
（1）物块落地时的速度大小；
（2）物块相对传送带滑动过程中，产生的热量Q。
轻弹簧AB长35cm，A端固定在重50N的物体上，该物体放在倾角为300的斜面上，如图所示，手执B端，使弹簧与斜面平行，当弹簧和物体沿斜面匀速下滑时，弹簧长变为40cm；当弹簧和物体沿斜面匀速上滑时，弹簧长度变为50cm，试求：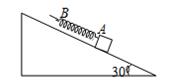
（1）求弹簧的劲度系数k；
（2）物体与斜面间的动摩擦因数μ．