下图是用直流发电机为保温室中电热器供电的电路图，直流发电机的电动势为250V，内阻为0.50Ω，输电线电阻R1=R2=1.0Ω。保温室中装有若干只完全相同的电热器用来调节室温，每只电热器的额定电压为200V，额定功率为1000W，其他电阻不计，也不考虑电热器电阻随温度的变化。求：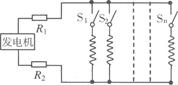
(1)为使电热器能正常工作，应接入多少个电热器；
(2)在电热器正常工作状态下，直流发电机对保温室供热的效率；
(3)保温室内的电热器可能消耗的最大电功率。
如图所示，轨道ABCD的AB段为一半径R=0.2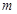
的光滑1/4圆形轨道，BC段为高为h=5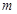的竖直轨道，CD段为水平轨道。一质量为0.1
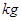的小球由A点从静止开始下滑到B点时速度的大小为2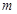/s，离开B点做平抛运动（g取10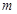/s2），求：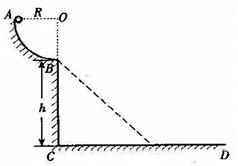
①小球离开B点后，在CD轨道上的落地点到C的水平距离；
②小球到达B点时对圆形轨道的压力大小？
③如果在BCD轨道上放置一个倾角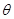
＝45°的斜面（如图中虚线所示），那么小球离开B点后能否落到斜面上？如果能，求它第一次落在斜面上的位置。
如图所示，长为R的轻质杆（质量不计），一端系一质量为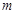
的小球（球大小不计），绕杆的另一端O在竖直平面内做匀速圆周运动，若小球最低点时，杆对球的拉力大小为1.5
，求：
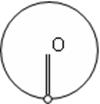
（1）小球最低点时的线速度大小？
（2）小球以多大的线速度运动，通过最高处时杆对球不施力？
宇航员站在一星球表面上的h高处,沿水平方向抛出一个小球,经过时间t,小球落到星球表面,测得抛出点与落地点之间的距离为L;若抛出时的初速度增大两倍,则抛出点与落地点之间的距离变为
L . 已知两落地点在同一水平面上.求该星球表面的重力加速度.
小船在静水中的划速为0.5m/s，水的流速为0.3m/s，河宽120m。
①小船怎样才能沿最短路径渡过河去？渡河需时间多少？
②小船怎样才能以最短时间渡过河去？需时间多少？
一个连同装备共有100kg的航天员，脱离宇宙飞船后，在离飞船45 m位置与飞船处于相对静止的状态，装备中有一个高压贮氧筒，能以50m/s速度喷出气体。
①航天员为了能在10min时间内返回飞船，估算他需要在开始返回的瞬间一次性向后喷出多少气体？
②假设他在开始返回的瞬时释放0.1 kg的氧气，估算则他需要多长时间返回宇宙飞船？ 返回宇宙飞船这段时间需要呼吸多少氧气？（.宇航员呼吸的耗氧率为2.5×10－4kg/s，）