已知地球的质量为M,半径为R,自转周期为T,地球表面处的重力加速度为g。地球同步卫星的质量为m,离地面的高度为h。利用上述物理量,可推算出地球同步卫星的环绕速度表达式为
A. |
B. |
C. |
D. |
如图所示,轻弹簧的一端固定在竖直墙上,质量为m的光滑弧形槽固定在光滑水平面上,弧形槽底端与水平面相切,一个质量也为m的小物块从槽高h处开始自由下滑,下列说法正确的是()
| A.在下滑过程中,物块的机械能守恒 |
| B.物块与弹簧碰撞后,弹簧的最大弹性势能为mgh |
| C.物块被弹簧反弹后,能回到槽高h处 |
| D.物块对弧形槽底端的压力大小为mg+mv2/h |
一滑块在水平地面上沿直线滑行,t=0时其速度为2.0m/s。从此刻开始在滑块运动方向上再施加一水平拉力F,力F和滑块的速度v随时间t的变化规律分别如图甲和乙所示。取g=10m/s2。则()
| A.滑块的质量为0.5kg |
| B.滑块与地面的动摩擦因数为0.4 |
| C.1~3s内,力F对滑块做功为8J |
| D.1~3s内,摩擦力对滑块做功为-8J |
沿x轴正向传播的一列简谐横波在t=0时刻的波形如图所示,P为介质中的一个质点,该波的传播速度为2.5m/s,则t=0.8s时()
| A.质点P受到的回复力方向指向y轴正方向 |
| B.质点P的速度方向指向y轴正方向 |
| C.质点P的速度方向与加速度的方向相同 |
| D.质点P的加速度方向指向y轴正方向 |
如图所示,一块橡皮用不可伸长的细线悬挂于O点,用铅笔靠着细线的左侧从O点开始水平向右匀加速移动,则在铅笔向右移动过程中,橡皮运动的速度()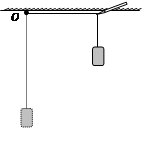
| A.大小和方向均不变 |
| B.大小不变,方向改变 |
| C.大小改变,方向不变 |
| D.大小和方向均改变 |
如图所示,在一辆由动力驱动的小车上有一水平放置的弹簧,其左端固定在小车上,右端与一小球相连。设在某一段时间内小球与小车相对静止且弹簧处于拉伸状态,若忽略小球与小车间的摩擦力,则在这段时间内小车可能是()
| A.向右做加速运动 |
| B.向右做减速运动 |
| C.向左做加速运动 |
| D.向左做减速运动 |