甲图为质谱仪的原理图.带正电粒子从静止开始经过电势差为U的电场加速后,从G点垂直于MN进入偏转磁场.该偏转磁场是一个以直线MN为上边界、方向垂直于纸面向外的匀强磁场,磁场的磁感应强度为B,带电粒子经偏转磁场后,最终到达照相底片上的H点.测得G、H间的距离为d,粒子的重力忽略不计.
(1)设粒子的电荷量为q,质量为m,试证明该粒子的比荷为: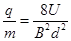 ;
;
(2)若偏转磁场的区域为圆形,且与MN相切于G点,如图乙所示,其它条件不变。要保证上述粒子从G点垂直于MN进入偏转磁场后不能打到MN边界上(MN足够长),求磁场区域的半径应满足的条件。
一物体以10m/s的初速水平抛出,不计空气阻力,g=10m/s2,求:
(1)抛出1s内物体下落的高度和水平位移分别是多少?
(2)抛出1s末物体的速度多大?速度方向与水平方向之间的夹角是多大?
带电粒子的质量 ,电荷量q=l.6×10-19C,以速度v=3.2×106m/s沿垂直于磁场同时又垂直于磁场边界的方向进入匀强磁场,磁场的磁感强度为B=0.17T.磁场的宽度为L=10cm.求:(不计重力)
,电荷量q=l.6×10-19C,以速度v=3.2×106m/s沿垂直于磁场同时又垂直于磁场边界的方向进入匀强磁场,磁场的磁感强度为B=0.17T.磁场的宽度为L=10cm.求:(不计重力)
(1)带电粒子离开磁场时的偏转角多大?
(2)带电粒子在磁场中运动的时间是多少?
(3)带电粒子在离开磁场时偏离入射方向的距离d多大?
如图所示 .在磁感应强度为 0.2T 的匀强磁场中 , 导体棒 AB 在金属框架上以 l0m/s 向右匀速滑动 , 金属框架的宽度为 0.5m. R1=R2="20" Ω .其它电阻不计 .求 
⑴流过导体棒 AB 的电流多大? 电流方向如何?
(2)R1上消耗的电功率是多少?
如图所示为一质谱仪的构造原理示意图,整个装置处于真空环境中,离子源N可释放出质量均为m、电荷量均为q(q>0)的离子.离子的初速度很小,可忽略不计.离子经S1、S2间电压为U的电场加速后,从狭缝S3进入磁感应强度大小为B、方向垂直于纸面向外的匀强磁场中,沿着半圆运动到照相底片上的P点处,测得P到S3的距离为x.求: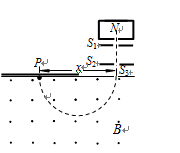
(1)离子经电压为U的电场加速后的速度v;
(2)离子的比荷(q/m)
如图8所示,在倾角为α的光滑金属导轨上,放置一根质量为m,长为L,通有电流I的导体棒.欲使导体棒静止在斜面轨道上,所加竖直向上的匀强磁场的磁感应强度B应为多大?