如图甲所示,一固定在地面上的足够长斜面,倾角为37°,物体A放在斜面底端挡板处,通过不可伸长的轻质绳跨过光滑轻质滑轮与物体B相连接,B的质量M=1kg,绳绷直时B离地面有一定高度。在t=0时刻,无初速度释放B,由固定在A上的速度传感器得到的数据绘出的A沿斜面向上运动的v-t图象如图乙所示,若B落地后不反弹,g取10 m/s2,sin37°=0.6,cos37°=0.8,则下列说法正确的是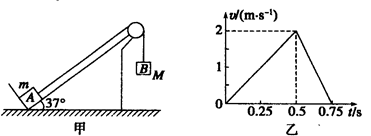
| A.B下落的加速度大小a=10m/s2 |
| B.A沿斜面向上运动的过程中,绳的拉力对A做的功W=3J |
| C.A的质量M=0.5Kg,A与斜面间的动摩擦因数μ=0.5 |
| D.0~0.75 s内摩擦力对A做的功0.75J |
一列简谐横波在某一时刻的波形图如图甲所示,图中P、Q两质点的横坐标分别为x=1.5 m和x=4.5 m.P点的振动图像如图乙所示.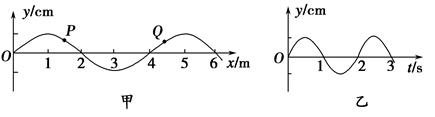
在下列四幅图中,Q点的振动图像可能是( ).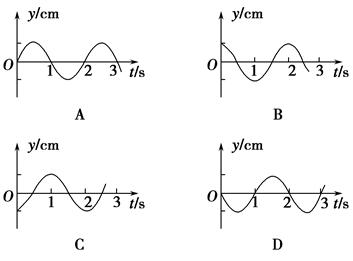
如图所示为一列简谐波在某一时刻的波形图,以下判断正确的是( ).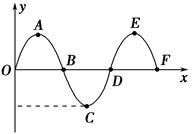
A.B、C两质点的振幅相同
B.C、E两质点的平衡位置间的距离为半个波长
C.A、C两质点的位移相同
D.波在A、B两质点间传播的时间为 周期
周期
如图所示,一列简谐横波沿x轴传播,实线和虚线分别是t1和t2时刻的波形图,已知t2-t1=1.0 s,由图判断下列哪一个波速是不可能的( ).
| A.1 m/s | B.3 m/s | C.5 m/s | D.10 m/s |
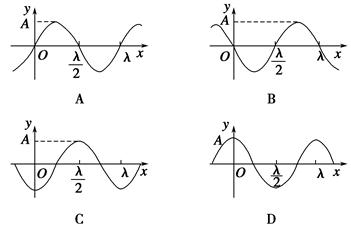
一简谐机械波沿x轴正方向传播,周期为T,波长为λ.若在x=0处质点的振动图像如图所示,则该波在t= 时刻的波形曲线为( ).
时刻的波形曲线为( ).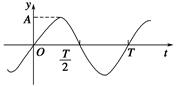
一列沿x轴正方向传播的简谐横波,某时刻的波形如图所示.P为介质中的一个质点,从该时刻开始的一段极短时间内,P的速度v和加速度a的大小变化情况是( ).
| A.v变小,a变大 | B.v变小,a变小 |
| C.v变大,a变大 | D.v变大,a变小 |