如图所示，固定在水平面上的斜面与水平面的连接处为一极小的光滑圆弧(物块经过Q点时不损失机械能)，斜面与地面是用同种材料制成的。斜面的最高点为P，P距离水平面的高度为h=5m。在P点先后由静止释放两个可视为质点的小物块A和B，A、B的质量均为m=1kg，A与斜面及水平面的动摩擦因数为μ1=0.5，B与斜面及水平面的动摩擦因数为μ2=0.3。A物块从P点由静止释放后沿斜面滑下，停在了水平面上的某处。
求：
(1)A物块停止运动的位置距离斜面的直角顶端O点的距离是多少?
(2)当A物块停止运动后准备再释放B物块时发现它们可能会发生碰撞，为了避免AB碰撞，此时对A另外施加了一个水平向右的外力F，把A物体推到了安全的位置，之后再释放B就避免了AB碰撞。求外力F至少要做多少功，可使AB不相撞?(g取10m/s2，此问结果保留三位有效数字)
一静止的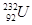
核转变为
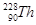核时放出一个α粒子，已知U232、Th228和α粒子的相对原子质量分别为M0、M1、M2，求放出的α粒子的初动能.
在原子反应堆中抽动液态金属或在医疗器械中抽动血液等导电液体时，由于不允许传动的机械部分与这些液体相接触，常使用一种电磁泵，如图所示为这种电磁泵的结构。导管放在磁场中，当电流通过导电液体时，这种液体即被驱动.如果导管中截面面积为ωh,磁场的宽度为L，磁感应强度为B，液体穿过磁场区域的电流强度为I，求驱动力造成的压强差为多少？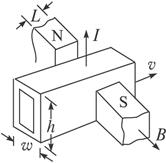
裂变反应是目前核能利用中常用的反应，以原子核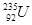
为燃料的反应堆中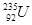，俘获一个慢中子后发生裂变反应可以有多种方式，其中一种方式可表示为：+
+
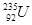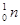
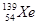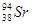+ 3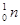
235.043 9 1.008 7 138.917 8 93.9154
反应方程下方的数字是中子及有关原子核静止时的质量（以原子质量u为单位），已知1 u的质量对应的能量为9.3×102 MeV,求放出的能量.
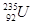受中子轰击时会发生裂变，产生
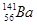和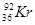
，同时放出200 MeV的能量.现要建设发电功率是5×105 kW的核电站，由铀235作为原子锅炉的燃料.假设核裂变释放的能量全部被用来发电，那么一天需纯铀235的质量为多大？（阿伏加德罗常数6.02×1023个/mol）
4个氢核聚变成一个氦核，同时放出两个正电子，释放出2.8×106eV的能量，列出核反应方程，并计算1 g氢核完成这个反应后释放出多少焦耳的能量.