如图所示,两平行金属导轨间的距离L=0.40 m,金属导轨所在平面与水平面夹角θ=37°,在导轨所在的平面内,分布着磁感应强度B=0.50 T、方向垂直于导轨所在平面的匀强磁场.金属导轨的一端接有电动势E=4.5 V、内阻r=0.50 Ω的直流电源.现把一个质量m=0.040 kg的导体棒ab放在金属导轨上,导体棒恰好静止.导体棒与金属导轨垂直且接触良好,导体棒与金属导轨接触的两点间的电阻R0=2.5 Ω,金属导轨电阻不计,g取10 m/s2.已知sin 37°=0.60,cos 37°=0.80,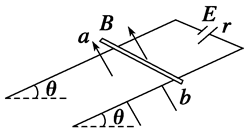
求:(1)通过导体棒的电流;
(2)导体棒受到的安培力大小;
(3)导体棒受到的摩擦力.
有两根外形基本相同的铁条,已知其中一根是永磁体,另一根是普通软铁,单凭视觉是无法将它们区分开的.若不用其他任何器材,如何才能把它们区分开来?
在以坐标原点 O为圆心、半径为 r的圆形区域内,存在磁感应强度大小为 B、方向垂直于纸面向里的匀强磁场,如图所示。一个不计重力的带电粒子从磁场边界与 x轴的交点 A处以速度 v沿-x方向射入磁场,它恰好从磁场边界与 y轴的交点 C处沿+y方向飞出。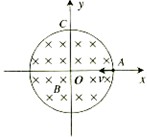
(1)请判断该粒子带何种电荷,并求出其比荷q/m ;
(2)若磁场的方向和所在空间范围不变,而磁感应强度的大小变为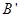 ,该粒子仍从 A处以相同的速度射入磁场,但飞出磁场时的速度方向相对于入射方向改变了60°角,求磁感应强度
,该粒子仍从 A处以相同的速度射入磁场,但飞出磁场时的速度方向相对于入射方向改变了60°角,求磁感应强度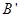 多大?此次粒子在磁场中运动所用时间 t是多少?
多大?此次粒子在磁场中运动所用时间 t是多少?
PQ为一根足够长的绝缘细直杆,处于竖直的平面内,与水平夹角为q斜放,空间充满磁感应强度B的匀强磁场,方向水平如图所示。一个质量为m,带有负电荷的小球套在PQ杆上,小球可沿杆滑动,球与杆之间的摩擦系数为m(m<tgq),小球带电量为q。现将小球由静止开始释放,试求小球在沿杆下滑过程中: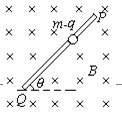
(1)小球最大加速度为多少?此时小球的速度是多少?
(2)下滑过程中,小球可达到的最大速度为多大?
如图所示,直角三角形ABC的斜边倾角为30°,底边BC长2L,处在水平位置,斜边AC是光滑绝缘的,在底边中点O处放置一正电荷Q,一个质量为m、电荷量为q的带负电的质点从斜面顶端A沿斜边滑下,滑到斜边的垂足D时速度为v[将(1)、(2)题正确选项前的标号填在括号内]
(1)在质点的运动中不发生变化的是( )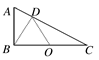
①动能
②电势能与重力势能之和
③动能与重力势能之和
④动能、电势能、重力势能之和
A.①② B.②③
C.④ D.②
(2)质点的运动是( )
A.匀加速运动
B.匀减速运动
C.先匀加速后匀减速的运动
D.加速度随时间变化的运动
(3)该质点滑到非常接近斜边底端C点时速率vc为多少?此时沿斜面向下的加速度aC为多少?
如图所示,一质量为m的塑料球形容器放在桌面上,它的内部有一劲度系数为k的轻弹簧,弹簧直立地固定于容器内壁的底部,弹簧上端经绝缘体系住一只带正电q、质量也为m的小球.从加一个竖直向上的场强为E的匀强电场起,到容器对桌面压力减为零时为止,求:
(1)小球的电势能改变量;
(2)容器对桌面压力减为零时小球的速度大小.