如图所示,光滑固定轨道的两端都是半径为R的四分之一圆弧,在轨道水平面上有两个质量均为m的小球B、C,B、C用一长度锁定不变的轻小弹簧栓接,弹性势能 .一质量也为m的小球A从左侧的最高点自由滑下,A滑到水平面与B碰后立即粘在一起结合成D就不再分离(碰撞时间极短).当D、C一起刚要滑到右侧最低点时,弹簧锁定解除且立即将C弹出并与弹簧分离.求
.一质量也为m的小球A从左侧的最高点自由滑下,A滑到水平面与B碰后立即粘在一起结合成D就不再分离(碰撞时间极短).当D、C一起刚要滑到右侧最低点时,弹簧锁定解除且立即将C弹出并与弹簧分离.求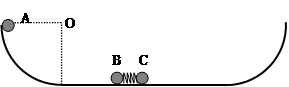
(1)弹簧锁定解除前瞬间,D、C速度大小
(2)弹簧锁定解除后,C第一次滑上轨道右侧圆弧部分的轨迹所对的圆心角
(3)弹簧锁定解除后,若C、D(含弹簧)每次碰撞均在水平面;求第N次碰撞结束时,C、D的速度
如图所示的U—I图象中,I是电源的路端电压随电流变化的图象,Ⅱ是某电阻两端的电压随电流变化的图象,当该电源向该电阻供电时,求电阻上消耗的功率和电源的效率分别为多少?
如图所示,真空有一个半径r=0.5m的圆形磁场,与坐标原点相切,磁场的磁感应强度大小B=2×10-3T,方向垂直于纸面向外,在x=r处的右侧有一个方向竖直向上的宽度为L1=0.5m的匀强电场区域(电场区域的左右边界如图中虚线所示),电场强度E=1.5×103N/C。在x=2m处有一垂直x方向的足够长的荧光屏,从O点处向不同方向发射出速率相同的荷质比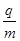 =1×109C/kg带正电的粒子,粒子的运动轨迹在纸面内,一个速度方向沿y轴正方向射入磁场的粒子,恰能从磁场与电场的相切处进入电场。不计重力及阻力的作用。求:
=1×109C/kg带正电的粒子,粒子的运动轨迹在纸面内,一个速度方向沿y轴正方向射入磁场的粒子,恰能从磁场与电场的相切处进入电场。不计重力及阻力的作用。求:
(1)该粒子进入电场时的速度和粒子在磁场中的运动时间。
(2)该粒子最后打到荧光屏上,该发光点的位置坐标。
(3)求荧光屏上出现发光点的范围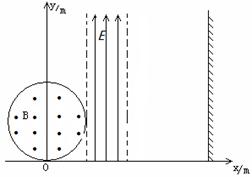
某兴趣小组设计了一种实验装置,用来研究碰撞问题,其模型如右图所示。用完全相同的轻绳将N个大小相同、质量不等的小球并列悬挂于一水平杆,球间有微小间隔,从左到右,球的编号依次为1、2、3…….N,球的质量依次递减,每个球的质量与其相邻左球质量之比为k(k<1)。将1号球向左拉起,然后由静止释放,使其与2号球碰撞,2号球再与3号球碰撞……所有碰撞皆为无机械能损失的正碰。并假设所有的球作为主动球完成一次碰撞后均由于某种原因与绳脱离并作自由落体运动。(不计空气阻力,忽略绳的伸长,g取10 m/s2)
(1)设与n+1号球碰撞前,n号球的速度为vn,求n+1号球被碰撞后瞬间的速度。
(2)若N=5,在1号球向左拉高h的情况下,要使5号球碰撞后升高16h(16h小于绳长),问k值为多少?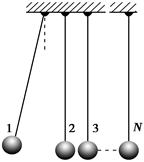
在如图所示的倾角为θ的光滑斜面上,存在着两个磁感应强度大小为B的匀强磁场,区域I的磁场方向垂直斜面向上,区域Ⅱ的磁场方向垂直斜面向下,磁场的宽度均为L,一个质量为m、电阻为R、边长也为L的正方形导线框,由静止开始沿斜面下滑,t1时 ab边刚越过GH进入磁场Ⅰ区,此时线框恰好以某一速度做匀速直线运动;t2时ab边下滑到JP与MN的中间位置,此时线框又恰好以另一速度做匀速直线运动。重力加速度为g,求:
(1)t1时刻线框具有的速度大小;
(2)t2时刻线框具有的速度大小;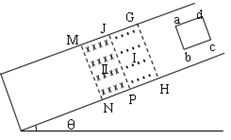
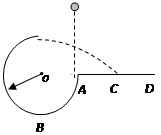
如图所示,竖直平面内的3/4圆弧形光滑管道半径略大于小球半径,管道中心到圆心距离为R,A端与圆心O等高,AD为水平面,B端在O的正下方,小球自A点正上方由静止释放,自由下落至A点时进入管道,当小球到达B点时,管壁对小球的弹力大小为小球重力大小的9倍。求:
(1)释放点距A点的竖直高度;(2)落点C与A的水平距离。