如图所示，在平面直角坐标系中，M是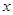
轴正半轴上一点，⊙M与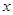轴的正半轴交于A、B两点，A在B的左侧，且OA、OB的长是方程
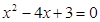的两根，ON是⊙M的切线，N为切点，N在第四象限．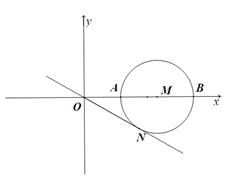
（1）求⊙M的直径；
（2）求直线ON的函数关系式；
（3）在轴上是否存在一点T，使△OTN是等腰三角形？若存在，求出T的坐标；若不存在，请说明理由．
甲乙两人准备整理一批新到的实验器材，若甲单独整理需要40分钟完工；若甲乙共同整理20分钟后，乙需单独整理20分钟才能完工.
(1)问乙单独整理多少分钟完工？
（2）若乙因工作需要，他的整理时间不超过30分钟，则甲至少整理多少分钟才能完工？
肇庆市某施工队负责修建1800米的绿道，为了尽量减少施工对周边环境的影响，实际工作效率比原计划提高了20%，结果提前两天完成．求原计划平均每天修绿道的长度．
在社区全民活动中，父子俩参加跳绳比赛.相同时间内父亲跳180个，儿子跳210个，已知儿子每分钟比父亲多跳20个，问父亲、儿子每分钟各跳多少个？
七（1）班的大课间活动丰富多彩，小峰与小月进行跳绳比赛.在相同的时间内，小峰跳了100个，小月跳了110个.如果小月比小峰每分钟多跳20个，试求出小峰每分钟跳绳多少个？
为创建“国家卫生城市”，进一步优化市中心城区的环境，德州市政府拟对部分路段的人行道地砖、花池、排水管道等公用设施全面更新改造，根据市政建设的需要，须在60天内完成工程．现在甲、乙两个工程队有能力承包这个工程．经调查知道：乙队单独完成此项工程的时间比甲队单独完成多用25天，甲、乙两队合作完成工程需要30天，甲队每天的工程费用2500元，乙队每天的工程费用2000元．
（1）甲、乙两个工程队单独完成各需多少天？
（2）请你设计一种符合要求的施工方案，并求出所需的工程费用．