如图所示，一个半球形的碗放在桌面上，碗口水平，O点为其球心，碗的内表面及碗口是光滑的.一根细线跨在碗口上，线的两端分别系有质量为m1和m2的小球，当它们处于平衡状态时，质量为m1的小球与O点的连线与水平线的夹角为α=60°.两小球的质量比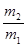
为 ( )
A． |
B． |
C． |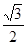
D． |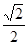
质量不计的轻质弹性杆P插在桌面上，杆端套有一个质量为m的小球沿水平方向做半径为R的匀速圆周运动，角速度为
，如图所示，则杆的上端受到的作用力大小为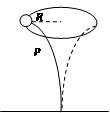
A． |
B． |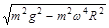
C． |
| D．不能确定 |
下列说法符合史实的是
| A．牛顿发现了行星的运动规律 |
| B．开普勒发现了万有引力定律 |
| C．卡文迪许第一次在实验室里测出了万有引力常量 |
| D．牛顿发现了海王星和冥王星 |
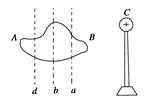
如图所示，左边是一个原先不带电的导体，右边C是后来靠近导体的带正电金属球，若用绝缘工具沿图示某条虚线将导体切开，分导体为A、B两部分，这两部分所带电荷量的数值分别为QA、QB，则下列结论正确的是
( )
| A．沿虚线d切开，A带负电，B带正电，且QB>QA[ |
| B．只有沿虚线b切开，才有A带正电，B带负电，并QB＝QA |
| C．沿虚线a切开，A带正电，B带负电，且QB>QA |
| D．沿任意一条虚线切开，都有A带正电，B带负电，而QA、QB的值与所切的位置有关 |
如图甲所示，两个平行金属板P、Q竖直放置，两板间加上如图乙所示的电压，t＝0时，Q板比P板电势高5 V，此时在两板的正中央M点有一个电子，速度为零，电子在电场力作用下运动，使得电子的位置和速度随时间变化。假设电子始终未与两板相碰。在0＜t＜8×10－10s的时间内，这个电子处于M点的右侧，速度方向向左且大小逐渐减小的时间是( )
| A．0＜t＜2×10－10s |
| B．2×10－10s＜t＜4×10－10s |
| C．4×10－10s＜t＜6×10－10s |
| D．6×10－10s＜t＜8×10－10s |
如图所示，为了科学研究的需要，常常将质子(11H)和α粒子(24He)等带电粒子储存在圆环状空腔中，圆环状空腔置于一个与圆环平面垂直的匀强磁场(偏转磁场)中，磁感应强度为B.如果质子和α粒子在空腔中做圆周运动的轨迹相同(如图中虚线所示)，偏转磁场也相同，则质子和α粒子在圆环状空腔中运动的动能EH和Eα、运动的周期TH和Tα的大小关系是 ( )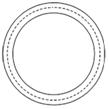 
| A．EH＝Eα，TH≠Tα | B．EH＝Eα，TH＝Tα |
| C．EH≠Eα，TH≠Tα | D．EH≠Eα，TH＝Tα |