如下图所示,在水平粗糙横杆上,有一质量为m的小圆环A,用一细线悬吊一个质量为m的球B。现用一水平拉力缓慢地拉起球B,使细线与竖直方向成37°角,此时环A仍保持静止(sin37°=0.6,cos37°=0.8),求: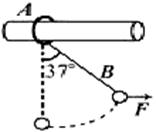
(1)此时水平拉力F的大小;
(2)环对横杆的压力及环受到的摩擦力。
(本题10分)在十字路口,汽车以 的加速度从停车线启动做匀加速运动,恰好有一辆自行车以
的加速度从停车线启动做匀加速运动,恰好有一辆自行车以 的速度匀速驶过停车线与汽车同方向行驶,求:
的速度匀速驶过停车线与汽车同方向行驶,求:
(1)什么时候它们相距最远?最远距离是多少?
(2)在距离停车线多远处汽车追上自行车?追到时汽车的速度是多大?
(12分)某人离公共汽车尾部20m,以速度v向汽车匀速跑过去,与此同时,汽车以1m/s2的加速度从静止启动,作匀加速直线运动。试问,此人的速度v分别为下列数值时,能否追上汽车?如果能,要用多长时间?如果不能,则他与汽车之间的最小距离是多少?
(1)v=6m/s;
(2)v=7m/s.
跳伞运动员在空中的运动可分为两个阶段:开始一段伞未张开,可近似看成自由落体运动,,伞张开后,则做匀减速运动。设运动员的初始高度为1500m ,第一段的下落高度为500m ,g取10 m/s2,试求:
(1)张开伞的一瞬间,运动员的速度大小
(2)要运动员充分安全地着地(即着地速度趋于零),第二阶段的合适加速度应是多大?
汽车从静止开始作匀加速直线运动,4s末关闭发动机,再经6s停下,10s内共行驶了30m.求:
(1)汽车运动中的最大速度;
(2)汽车在两段运动过程中的加速度大小。
如图所示,皮球以速度8m/s向右运动,与墙相撞后以速度4m/s反弹回来,设皮球与墙相撞时间为0.1s,求皮球撞墙过程中加速度?