如图所示，一个质量为0.6kg的小球以某一初速度从P点水平抛出，恰好从光滑圆弧AB的A点的切线方向进入圆弧(不计空气阻力，进入圆弧时无机械能损失)，并从最低点B通过一段光滑小圆弧滑上另一粗糙斜面CD。已知圆弧AB的半径R=0.9m,θ=600,B在O点正下方，斜面足够长，动摩擦因数u=0.5，斜面倾角为370，小球从p到达A点时的速度为4m/s。（g取10m/s2，cos37°=0.8，sin37°=0.6）问：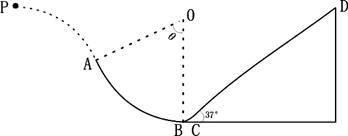
（1）P点与A点的水平距离和竖直高度
（2）小球在斜面上滑行的总路程
内壁光滑的导热气缸竖直浸放在盛有冰水混合物的水槽中，用不计质量的活塞封闭压强为1.0×105 Pa、体积为2.0×10－3 m3的理想气体．现在活塞上方缓缓倒上沙子，使封闭气体的体积变为原来的一半，然后将汽缸移出水槽，缓慢加热，使气体温度变为127 ℃.(大气压强为1.0×105 Pa)
①求汽缸内气体的最终体积（保留三位有效数字）；
②在右图所示的p－V图上画出整个过程中汽缸内气体的状态变化．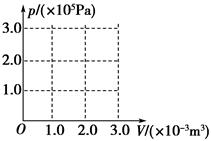
(18分)玩具小车连同固定在小车上的水平皮带运输机总质量M=2kg，静止在光滑水平面上；皮带顺时针转动，相对小车的速度保持为
=3m/s；可视为质点的带正电小物块质量m＝1kg，电荷量q=0.01C，以水平初速
＝9m/s从皮带左端滑上皮带；皮带与小物块间动摩擦因数
＝0.8，设整个装置绝缘，小物块在运动过程中q保持不变，g取10m/s2。
（1）若皮带足够长，求小物块刚滑上传送带时，物块、小车的加速度大小？小车最终能达到最大速度？
（2）小车右侧足够远处有一内壁光滑、绝缘的竖直圆形轨道，其半径R="0.25m" 。轨道最下端C点与AB等高，C点处有一小缺口，可以让绝缘小物块射入圆形轨道内。小物块以
＝5m/s的速度从C处的小缺口冲入圆轨道，在其冲入瞬间，轨道所在空间立即施加一竖直方向的匀强电场。若要使小物块不脱离圆轨道，则匀强电场的大小与方向应满足什么条件？
(18分) 在直角坐标系第一象限与第三象限分布有如图所示的匀强磁场和匀强电场，电场强度为E、磁感应强度为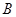
；现在第三象限中从P点以初速度
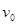沿x轴方向发射质量为
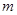，带
的离子，离子经电场后恰从坐标原点O射入磁场。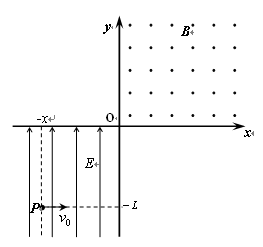
（1）已知P点的纵坐标为
，试求P点的横坐标x；
（2）若离子经O点射入磁场时的速度为2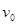，试求离子在磁场中运动的时间及磁场出射点距O点的距离d。
用轻弹簧竖直悬挂一质量未知的铁块，静止时弹簧伸长量为L，现将铁块置于倾斜木板上，用该弹簧沿木板向上匀速拉动铁块，此时弹簧的伸长量仍为 L ,已知木板与水平方向的夹角 θ=30°，则可测出铁块与木板间的动摩擦因数为多大？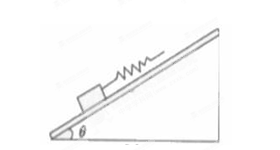
如图所示，长为20cm的轻绳BC两端固定在天花板上，在中点系上一重60N的物体 ．试求：（1）当BC的距离为10cm时，AB段绳上的拉力为多少；
（2）当BC的距离为10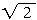
cm时，AB段绳上的拉力为多少.