设命题甲:关于 的不等式
的不等式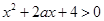 对一切
对一切 恒成立,命题乙:对数函数
恒成立,命题乙:对数函数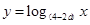 在
在 上递减,那么甲是乙的( )
上递减,那么甲是乙的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
下列推理是归纳推理的是( )
| A.A,B为定点,动点P满足|PA|+|PB|=2a>|AB|,则P点的轨迹为椭圆 |
| B.由a1=1,an=3n-1,求出S1,S2,S3,猜想出数列的前n项和Sn的表达式 |
C.由圆x2+y2=r2的面积πr2,猜想出椭圆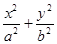 =1的面积S=πab =1的面积S=πab |
| D.利用等差数列的性质推理得到等比数列的相关性质 |
设全集U={1,2,3,4},则集合A="{1," 3},则CUA=()
| A.{1, 4} | B.{2, 4} | C.{3, 4} | D.{2, 3} |
如图所示,在正方体ABCD-A1B1C1D1中,E,F分别为棱AA1,CC1的中点,则在空间中与直线A1D1,EF,CD都相交的直线( ).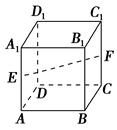
| A.有无数条 | B.有且只有两条 | C.有且只有三条 | D.不存在 |
a,b,c表示三条不重合的直线,M表示平面,给出下列四个命题:①若a∥M,b∥M,则a∥b;②若b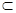 M,a∥b,则a∥M;③若a⊥c,b⊥c,则a∥b;④若a⊥M,b⊥M,则a∥b.其中正确命题的个数有
M,a∥b,则a∥M;③若a⊥c,b⊥c,则a∥b;④若a⊥M,b⊥M,则a∥b.其中正确命题的个数有
| A.0个 | B.1个 | C.2个 | D.3个 |
如图所示,点P在正方形ABCD所在平面外,PA⊥平面ABCD,PA=AB,则PB与AC所成的角是( )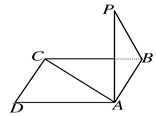
| A.90° | B.60° |
| C.45° | D.30° |