已知函数 .
.
(Ⅰ)当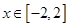 时,
时, 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(Ⅱ)若对一切 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
某班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
| 积极参加班级工作 |
不太主动参加班级工作 |
合计 |
|
| 学习积极性高 |
18 |
7 |
25 |
| 学习积极性一般 |
6 |
19 |
25 |
| 合计 |
24 |
26 |
50 |
(1)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(2)试运用独立性检验的思想方法分析:学生的学习积极性与对待班级工作的态度是否有关系?说明理由.
 |
0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
袋子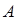 和
和 中装有若干个均匀的红球和白球,从
中装有若干个均匀的红球和白球,从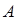 中摸一个红球的概率是
中摸一个红球的概率是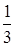 ,从
,从 中摸出一个红球的概率为
中摸出一个红球的概率为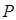 .
.
⑴从A中有放回地摸球,每次摸出一个,有3次摸到红球则停止.
①求恰好摸5次停止的概率;
② 记5次之内(含5次)摸到红球的次数为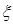 ,求随机变量
,求随机变量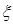 的分布列及数学期望
的分布列及数学期望 .
.
⑵若A、B两个袋子中的球数之比为1:2,将A、B中的球装在一起后,从中摸出一个红球的概率是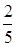 ,求
,求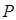 的值.
的值.
将长为1 的棒任意地折成三段,求三段的长度都不超过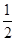 的概率.
的概率.
为了检测某种产品的质量,抽取了一个容量为100的样本,数据的分组数如下: ;
;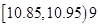 ;
; ;
; ;
;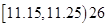 ;
;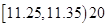 ;
;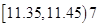 ;
; ;
; ;
;
(1)列出频率分布表(含累积频率);
(2)画出频率分布直方图以及频率分布折线图;
(3)据上述图表,估计数据落在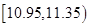 范围内的可能性是百分之几?
范围内的可能性是百分之几?
(4)数据小于11.20的可能性是百分之几?
解不等式