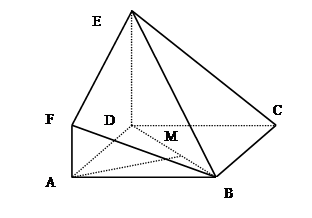
如图, 是边长为3的正方形,
是边长为3的正方形,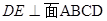 ,
,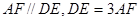 ,
,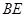 与平面
与平面 所成的角为
所成的角为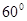 .
.
(1)求二面角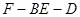 的的余弦值;
的的余弦值;
(2)设点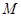 是线段
是线段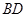 上一动点,试确定
上一动点,试确定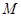 的位置,使得
的位置,使得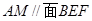 ,并证明你的结论.
,并证明你的结论.
(本小题满分12分)设命题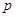 :关于
:关于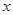 的不等式
的不等式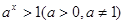 的解集为
的解集为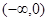 ;命题
;命题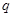 :函数
:函数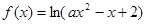 的定义域是
的定义域是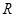 .如果命题“
.如果命题“ ”为真命题,“
”为真命题,“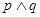 ”为假命题,求
”为假命题,求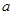 的取值范围.
的取值范围.
(本小题满分12分)已知集合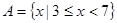 ,
,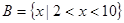 ,
,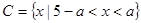 .
.
(1)求 ,
,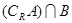 ;
;
(2)若“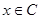 ”是“
”是“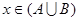 ”的充分条件,求
”的充分条件,求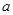 的取值范围.
的取值范围.
(本小题满分12分)已知角 的终边在第二象限,且与单位圆交于点
的终边在第二象限,且与单位圆交于点 .
.
(1)求实数 的值;
的值;
(2)求 的值.
的值.
已知函数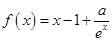 (
(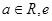 为自然对数的底数).
为自然对数的底数).
(1)若曲线 在点
在点 处的切线平行于
处的切线平行于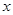 轴,求
轴,求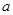 的值;
的值;
(2)讨论函数 的极值情况;
的极值情况;
(3)当 时,若直线
时,若直线 与曲线
与曲线 没有公共点,求k的取值范围.
没有公共点,求k的取值范围.
已知椭圆E的长轴的一个端点是抛物线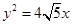 的焦点,离心率是
的焦点,离心率是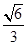 .
.
(1)求椭圆E的标准方程;
(2)已知动直线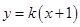 与椭圆E相交于A、B两点,且在
与椭圆E相交于A、B两点,且在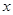 轴上存在点M,使得
轴上存在点M,使得 与k的取值无关,试求点M的坐标.
与k的取值无关,试求点M的坐标.