如图，等腰梯形ABCD放置在平面直角坐标系中，已知A（-2，0）、B（6，0）、A（0，3），反比例函数的图象经过点C．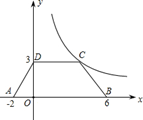
（1）求C点坐标和反比例函数的解析式；
（2）将等腰梯形ABCD向上平移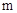
个单位后，使点B恰好落在双曲线上，求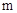的值．
如图，在△ABC中，CD⊥AB于D，AC＝20，BC＝15，DC＝12。
(1)求AB的长。
（2）判断△ABC的形状，并说明理由。
先化简,再求值: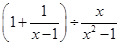 
，选一个你喜欢的数字代入求值。
解分式方程：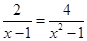 
计算：(1)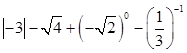
如图，在平面直角坐标系中，直线y=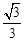
x+1分别与两坐标轴交于B，A两点，C为该直线上的一动点，以每秒1个单位长度的速度从点A开始沿直线BA向上移动，作等边△CDE，点D和点E都在x轴上，以点C为顶点的抛物线y=a（x﹣m）2+n经过点E．⊙M与x轴、直线AB都相切，其半径为3（1﹣
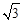）a．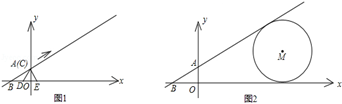
（1）求点A的坐标和∠ABO的度数；
（2）当点C与点A重合时，求a的值；
（3）点C移动多少秒时，等边△CDE的边CE第一次与⊙M相切？