如图,抛物线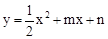 与x轴交于A、B两点,与y轴交于C点,四边形OBHC为矩形,CH的延长线交抛物线于点D(5,2),连结BC、AD.
与x轴交于A、B两点,与y轴交于C点,四边形OBHC为矩形,CH的延长线交抛物线于点D(5,2),连结BC、AD.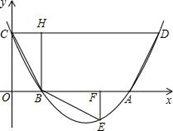
(1)求C点的坐标及抛物线的解析式;
(2)将△BCH绕点B按顺时针旋转90°后再沿x轴对折得到△BEF(点C与点E对应),判断点E是否落在抛物线上,并说明理由;
(3)设过点E的直线交AB边于点P,交CD边于点Q.问是否存在点P,使直线PQ分梯形ABCD的面积为1∶3两部分?若存在,求出P点坐标;若不存在,请说明理由.
如图,菱形ABCD的对角线AC,BD相交于点O,点E,F分别是边AB,AD的中点.
(1)请判断△OEF的形状,并证明你的结论;
(2)若AB=13,AC=10,请求出线段EF的长.
如图,已知点D在双曲线 (
( )的图象上,以D为圆心的⊙D与y轴相切于点C(0,4),与x轴交于A,B两点,抛物线
)的图象上,以D为圆心的⊙D与y轴相切于点C(0,4),与x轴交于A,B两点,抛物线 经过A,B,C三点,点P是抛物线上的动点,且线段AP与BC所在直线有交点Q.
经过A,B,C三点,点P是抛物线上的动点,且线段AP与BC所在直线有交点Q.
(1)写出点D的坐标并求出抛物线的解析式;
(2)证明∠ACO=∠OBC;
(3)探究是否存在点P,使点Q为线段AP的四等分点?若存在,求出点P的坐标;若不存在,请说明理由.
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D以每秒1个单位长度的速度由点A向点B匀速运动,到达B点即停止运动,M,N分别是AD,CD的中点,连接MN,设点D运动的时间为t.
(1)判断MN与AC的位置关系;
(2)求点D由点A向点B匀速运动的过程中,线段MN所扫过区域的面积;
(3)若△DMN是等腰三角形,求t的值.
下列网格中的六边形ABCDEF是由边长为6的正方形左上角剪去边长为2的正方形所得,该六边形按一定的方法可剪拼成一个正方形.
(1)根据剪拼前后图形的面积关系求出拼成的正方形的边长;
(2)如图甲,把六边形ABCDEF沿EH,BG剪成①②③三部分,请在图甲中画出将②③与①拼成的正方形,然后标出②③变动后的位置,并指出②③属于旋转、平移和轴对称中的哪一种变换;
(3)在图乙中画出一种与图甲不同位置的两条裁剪线,并在图乙中画出将此六边形剪拼成的正方形.
如图,在菱形ABCD中,M,N分别是边AB,BC的中点,MP⊥AB交边CD于点P,连接NM,NP.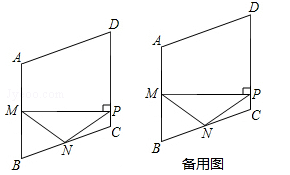
(1)若∠B=60°,这时点P与点C重合,则∠NMP= 度;
(2)求证:NM=NP;
(3)当△NPC为等腰三角形时,求∠B的度数.