如图，绝缘水平地面上有宽L=0.4m的匀强电场区域，场强
，方向水平向左。带电的物块B静止在电场边缘的O点，带电量
、质量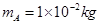
的物块A在距O点s=2.25m处以vo=5m/s的水平初速度向右运动，并与B发生碰撞，假设碰撞前后A、B构成的系统没有动能损失。A的质量是B的k(k>1)倍，A、B与地面间的动摩擦因数都为
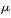=0.2，物块均可视为质点，且A的电荷量始终不变，取g = 10m/S2。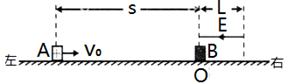
(1) 求A到达O点与B碰撞前的速度大小；
(2) 求碰撞后瞬间A和B的速度大小；
(3) 讨论K在不同取值范围时电场力对A做的功。
如图所示，位于竖直平面内的光滑轨道，由一段斜的直轨道和与之相切的圆形轨道连接而成，圆形轨道的半径为R．一质量为m的小物块从斜轨道上某处由静止开始下滑，然后沿圆形轨道运动．要求物块能通过圆形轨道最高点，且在该最高点与轨道间的压力不能超过５mg(g为重力加速度)，求物块初始位置相对于圆形轨道底部的高度h的取值范围．
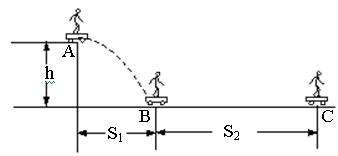
某滑板爱好者在离地h=1.8m高的平台上滑行，水平离开A点后落在水平地面上的B点，其水平位移S1=3.6m．着地时由于存在能量损失，着地后速度变为v=4m/s，并以此为初速沿水平地面滑行S2=8m后停止．已知人与滑板的总质量m=60kg．试求：
（1）人与滑板在水平地面滑行时受到的平均阻力的大小；
（2）人与滑板离开平台时的水平初速度大小（空气阻力忽略不计，取当地的重力加速度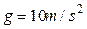
）．
已知地球表面的重力加速度为g=10m/s2，地球半径为R=6.4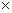
106m，求离地高度为地球半径3倍的人造地球卫星的线速度．
如图所示，光滑的1/4圆弧轨道AB、EF，半径AO、0′F均为R且水平．质量为m、长度也为R的小车静止在光滑水平面CD上，小车上表面与轨道AB、EF的末端B、E相切．一质量为m的物体(可视为质点)从轨道AB的A点由静止开始下滑，由末端B滑上小车，小车立即向右运动．当小车右端与壁DE刚接触时，物体m恰好滑动到小车右端且相对于小车静止，同时小车与壁DE相碰后立即停止运动但不粘连，物体继续运动滑上圆弧轨道EF，以后又滑下来冲上小车．求：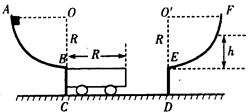
(1)物体m滑上轨道EF的最高点相对于E点的高度h
(2)水平面CD的长度;
(3)当物体再从轨道EF滑下并滑上小车后，小车立即向左运动．如果小车与壁BC相碰后速度也立即变为零，最后物体m停在小车上的Q点，则Q点距小车右端多远?
如图所示，绷紧的传送带与水平面的夹角θ=300，皮带在电动机的带动下，始终保持V="2" m/s的速率运行．现把一质量m="10" kg的工件(可看做质点)轻轻放在皮带的底端，经时间t="1.9" s，工件被传送到h="1.5" m的高处，取g="10" m/s2．求：
(1)工件与皮带间的动摩擦因数；
(2)电动机由于传送工件多消耗的电能