先化简,再求值: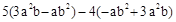 ,其中
,其中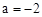 ,
,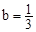 .
.
已知四边形ABCD各顶点的坐标分别是A(0,0),B(3,6),C(6,8),D(8,0)
(1)请建立适当的平面直角坐标系,并描出点A点、B点、C点、D点.
(2)求四边形ABCD的面积.
如图所示,已知AB∥CD ,BC∥DE,若∠B=55°,求∠D的度数.
学习完统计知识后,小兵就本班同学的上学方式进行调查统计.他通过收集数据后绘制的两幅不完整的统计图如下图所示.请你根据图中提供的信息解答下列问题:

(1)求该班共有多少名学生;
(2)请将表示“步行”部分的条形统计图补充完整;
(3)在扇形统计图中,“骑车”部分扇形所对应的圆心角是多少度;
(4)若全年级共1000名学生,估计全年级步行上学的学生有多少名.
解不等式组 ,并把其解集在数轴上表示出来.
,并把其解集在数轴上表示出来.
解方程组: .
.