小亮家距离学校8千米，昨天早晨，小亮骑车上学途中，自行车“爆胎”，恰好路边有“自行车”维修部，几分钟后车修好了，为了不迟到，他加快了骑车到校的速度．回校后，小亮根据这段经历画出如下图象．该图象描绘了小亮行的路程S与他所用的时间t之间的关系．请根据图象，解答下列问题：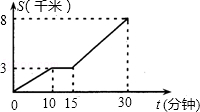
（1）小亮行了多少千米时，自行车“爆胎”？修车用了几分钟？
（2）小亮到校路上共用了多少时间？
（3）如果自行车没有“爆胎”，一直用修车前的速度行驶，那么他比实际情况早到或晚到学校多少分钟（精确到0.1）？
某车间接到加工200个零件的任务，在加工完40个后，由于改进了技术，每天加工的零件数量是原来的2.5倍，整个加工过程共用了13天完成．求原来每天加工零件的数量．
在一个不透明的盒子中放有三张卡片，分别标记为A、B、C，每张卡片除了标记不同外，其余均相同．某同学第一次从盒子中随机抽取一张卡片，卡片放回，第二次又随机抽取一张卡片．请用画树状图（或列表）的方法，求两次抽取的都是A的概率．
化简：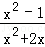
÷
．
两个直角边为6的全等的等腰直角三角形Rt△AOB和Rt△CED，按如图一所示的位置放置，点O与E重合．
（1）Rt△AOB固定不动，Rt△CED沿x轴以每秒2个单位长度的速度向右运动，当点E运动到与点B重合时停止，设运动x秒后，Rt△AOB和Rt△CED的重叠部分面积为y，求y与x之间的函数关系式；
（2）当Rt△CED以（1）中的速度和方向运动，运动时间x=2秒时，Rt△CED运动到如图二所示的位置，若抛物线y=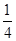
x2+bx+c过点A，G，求抛物线的解析式；
（3）现有一动点P在（2）中的抛物线上运动，试问点P在运动过程中是否存在点P到x轴或y轴的距离为2的情况？若存在，请求出点P的坐标；若不存在，请说明理由．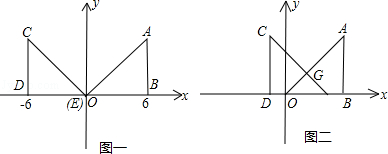
如图，已知直线AB与x轴、y轴分别交于A和B，OA=4，且OA、OB长是关于x的方程x2﹣mx+12=0的两实根，以OB为直径的⊙M与AB交于C，连接CM并延长交x轴于N．
（1）求⊙M的半径．
（2）求线段AC的长．
（3）若D为OA的中点，求证：CD是⊙M的切线．