如图所示,物块的质量m=30kg,细绳一端与物块相连,另一端绕过光滑的轻质定滑轮,当人用100N的力斜向下拉绳子时,滑轮两侧细绳与水平方向的夹角均为30°,物体在水平面上保持静止,滑轮上端的悬绳竖直(取g=10m/s2)。
求:(1)地面对物体的弹力大小和摩擦力大小;
(2)滑轮上方竖直悬绳的拉力大小。
(9分)如图所示,A、B两个木块质量分别为2 kg与0.9 kg,A、B与水平地面间接触光滑,上表面粗糙,质量为0.1 kg的铁块以10 m/s的速度从A的左端向右滑动,最后铁块与B的共同速度大小为0.5 m/s,求: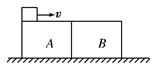
①A的最终速度;
②铁块刚滑上B时铁块的速度.
一列沿着X轴正方向传播的横波,在t=0时刻的波形如图甲所示。图甲中某质点的振动图象如图乙所示。求:
①该波的波速。
②甲图中的质点L从图示位置到波峰的时间。
③写出t =0开始计时x="2m" 处的振动方程
如图a所示,水平直线MN下方有竖直向上的匀强电场,现将一重力不计、比荷 =106 C/kg的正电荷置于电场中的O点由静止释放,经过
=106 C/kg的正电荷置于电场中的O点由静止释放,经过 ×10-5 s后,电荷以v0=1.5×104 m/s的速度通过MN进入其上方的匀强磁场,磁场与纸面垂直,磁感应强度B按图b所示规律周期性变化(图b中磁场以垂直纸面向外为正,以电荷第一次通过MN时为t=0时刻).求:
×10-5 s后,电荷以v0=1.5×104 m/s的速度通过MN进入其上方的匀强磁场,磁场与纸面垂直,磁感应强度B按图b所示规律周期性变化(图b中磁场以垂直纸面向外为正,以电荷第一次通过MN时为t=0时刻).求: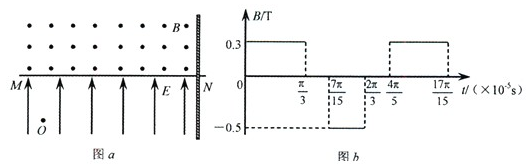
(1)匀强电场的电场强度E的大小;(保留2位有效数字)
(2)图b中t= ×10-5 s时刻电荷与O点的水平距离;
×10-5 s时刻电荷与O点的水平距离;
(3)如果在O点右方d=68 cm处有一垂直于MN的足够大的挡板,求电荷从O点出发运动到挡板所需的时间.(sin 37°=0.60,cos 37°=0.80) (保留2位有效数字)
2013年7月5日-12日,中俄“海上联合-2013”海上联合军事演习在日本海彼得大帝湾附近海空域举行。在某天进行的演习中,我国研发的一艘022型导弹快艇以30m/s的恒定速度追击前面同一直线上正在以速度v1逃跑的假想敌舰。当两者相距L0=2km时,以60m/s相对地面的速度发射一枚导弹,假设导弹沿直线匀速射向假想敌舰,经过t1=50s艇长通过望远镜看到了导弹击中敌舰爆炸的火光,同时发现敌舰速度减小但仍在继续逃跑,速度变为v2,于是马上发出了第二次攻击的命令,第二枚导弹以同样速度发射后,又经t2=30s,导弹再次击中敌舰并将其击沉。不计发布命令和发射反应的时间,发射导弹对快艇速度没有影响,求敌舰逃跑的速度v1、v2分别为多大?
如图,ABC三个木块的质量均为m。置于光滑的水平面上,BC之间有一轻质弹簧,弹簧的两端与木块接触可不固连,将弹簧压紧到不能再压缩时用细线把BC紧连,是弹簧不能伸展,以至于BC可视为一个整体,现A以初速 沿BC的连线方向朝B运动,与B相碰并粘合在一起,以后细线突然断开,弹簧伸展,从而使C与A,B分离,已知C离开弹簧后的速度恰为
沿BC的连线方向朝B运动,与B相碰并粘合在一起,以后细线突然断开,弹簧伸展,从而使C与A,B分离,已知C离开弹簧后的速度恰为 ,求弹簧释放的势能。
,求弹簧释放的势能。