如图所示,绷紧的传送带与水平面的夹角θ=30°,传送带在电动机的带动下,始终保持v0=2 m/s的速率运行.现把一质量为m=1kg的工件(可看为质点)轻轻放在传送带的底端,经时间t=1.9 s,工件被传送到h=1.5 m的高处,并取得了与传送带相同的速度,取g=10 m/s2.求: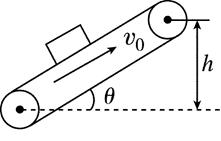
(1)工件与传送带之间的滑动摩擦力f
(2)工件与传送带之间的相对位移Δs
4×100m接力赛是奥运会上最为激烈的比赛项目,有甲乙两运动员在训练交接棒的过程中发现,甲短距离加速后能保持9m/s的速度跑完全程.为了确定乙起跑的时机,需在接力区前适当的位置 设置标记,在某次练习中,甲在接力区前s0 处作了标记,当甲跑到此标记时向乙发出起跑口令,乙在接力区的前端听到口令时立即起跑(忽略声音传播的时间及人的反应时间),已知接力区的长度为L=20m,设乙起跑后的运动是匀加速运动,试求:
设置标记,在某次练习中,甲在接力区前s0 处作了标记,当甲跑到此标记时向乙发出起跑口令,乙在接力区的前端听到口令时立即起跑(忽略声音传播的时间及人的反应时间),已知接力区的长度为L=20m,设乙起跑后的运动是匀加速运动,试求:
(1)若s0 =13.5m,且乙恰好在速度达到与甲相同时被甲追上,完成交接棒,则在完成交接棒时乙离接力区末端的距离为多大?
(2)若s0 =16m,乙的最大速度为8m/s,并能以最大速度跑完全程,要使甲乙能在接力区完成交接棒,则乙在听到口令后加速的加速度最大为多少?(结果保留3位有效数字)
在真空中,氢原子从能级A跃迁到能级B时,辐射出波长为λl的光子;从能级A跃迁到能级C时,辐射出波长为λ2的光子。若λ1>λ2,真空中的光速为c,那么氢原子从能级B跃迁到能级C时是辐射光子还是吸收光子,这个光子的波长为多少?
一个 氢原子的质量为1.6736×10-27kg,一个锂原子的质量
氢原子的质量为1.6736×10-27kg,一个锂原子的质量 为11.6505×10-27kg,一个氦原子的质量为6.6467×10-27kg。一个锂核受到一个质子轰击变为2个α粒子,(1)写出核反应方程,并计算该反应释放的核能是多少?(2)1mg锂原子发生这样的反应共释放多少核能?(结果保留3位有效数字)
为11.6505×10-27kg,一个氦原子的质量为6.6467×10-27kg。一个锂核受到一个质子轰击变为2个α粒子,(1)写出核反应方程,并计算该反应释放的核能是多少?(2)1mg锂原子发生这样的反应共释放多少核能?(结果保留3位有效数字)
一小球从楼顶边沿处自由下落,在到达地面前最后1s内通过的位移是楼高的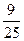 ,求楼高.(重力加速度g取10m/s2)
,求楼高.(重力加速度g取10m/s2)
如图,AB是倾角为θ的粗糙直轨道,BCD是光滑的圆弧轨道,AB恰好在B点与圆弧相切,圆弧的半径为R。一个质量为m的物体(可以看作质点)从直轨道上的P点由静止释放,结果它能在两轨道间做往返运动。已知P点与圆弧的圆心o等高,物体与轨道AB间的动摩擦因数为μ。求
(1)物体做往返运动的整个过程中在AB轨道上通过的总路程
(2)最终当物体通过圆弧轨道最低点E时,对圆弧轨道的压力
(3)为使物体能顺利到达圆弧轨道的最高点D释放点距B点的距离L应满足什么条件?