如图所示,质量为M的光滑长木板静止在光滑水平地面上,左端固定一劲度系数为k的水平轻质弹簧,右侧用一不可伸长的细绳连接于竖直墙上,细绳所能承受的最大拉力为FT,使一质量为m、初速度为v0的小物体,在木板上无摩擦地向左滑动而后压缩弹簧,细绳被拉断,不计细绳被拉断时的能量损失.弹簧的弹性势能表达式为Ep= kx2(k为弹簧的劲度系数,x为弹簧的形变量).
kx2(k为弹簧的劲度系数,x为弹簧的形变量).

(1)要使细绳被拉断,vo应满足怎样的条件?
(2)若小物体最后离开长木板时相对地面速度恰好为零,请在坐标系中定性画出从小物体接触弹簧到与弹簧分离的过程小物体的v—t图像;
(3)若长木板在细绳拉断后被加速的过程中,所能获得的最大加速度为aM,求此时小物体的速度.
何老师出去旅游,驾驶汽车以20m/s的速度在平直公路上匀速行驶,忽然发现正前方45m的十字路口A处的另一条平直小马路上,距离A处8 m远的一只小狗正以2m/s速度向A处匀速跑来。何老师为了避免撞上小狗,立即刹车,让小狗先通过路口。若何老师采取紧急刹车的反应时间为0.5s,则汽车刹车的加速度应满足什么条件才能保证安全?
如图所示,质量均为m的两个小球A、B套在光滑水平直杆P上,整个直杆被固定在竖直转轴上。两球用劲度系数为k、自然长度为L的轻质弹簧连接在一起,A球被轻质细绳拴在竖直转轴上,细绳长度也为L。现使杆P、A、B绕转轴在水平面内以角速度 匀速转动。求:稳定后细绳的拉力和弹簧的总长度。
匀速转动。求:稳定后细绳的拉力和弹簧的总长度。
如图所示,在水平地面上固定一倾角θ=37°、表面光滑的斜面,物体A以v1=6m/s的初速度沿斜面上滑,同时在物体A的正上方,物体B以某一初速度v2水平抛出。如果当A上滑到最高点时恰好被B物体击中(A、B均可看作质点, sin37°=0.6,cos37°=0.8,g取10m/s2)。
求:(1)物体A上滑到最高点所用的时间t;
(2)物体B抛出时的初速度v2;
(3)物体A、B间初始位置的高度差h。
某兴趣小组对一辆自制遥控小车的性能进行研究,他们让这辆小车在水平的直轨道上由静止开始运动,并将小车运动的全过程记录下来,通过处理转化为v-t图象,如图所示(除2~10s内的图象为曲线外,其余时间段图象均为直线)。小车运动的过程中2~14s时间段内小车的功率保持不变,在14s末停止遥控而让小车自由滑行。已知小车的质量为1kg,在整个运动过程中小车所受到的阻力大小不变。求: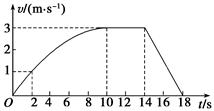
(1)小车所受到的阻力大小;
(2)0~2s时间内电动机提供的牵引力大小;
(3)小车匀速行驶阶段的功率。
质量为0.2 kg的弹性球从空中某高度由静止开始下落,该下落过程对应的 图象如图所示。球与水平地面相碰后离开地面时的速度大小为碰撞前的3/4。设球受到的空气阻力大小恒为f,取
图象如图所示。球与水平地面相碰后离开地面时的速度大小为碰撞前的3/4。设球受到的空气阻力大小恒为f,取 =10m/s2,求:
=10m/s2,求:
(1)弹性球受到的空气阻力f的大小;
(2)弹性球第一次碰撞后反弹的高度h。